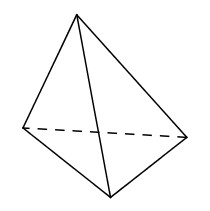
Giải bài 1 trang 12 SGK Hình học 12Chứng minh rằng một đa diện có các mặt là những tam giác thì tổng số các mặt của nó là một số chẵn. Cho ví dụ Đề bài Chứng minh rằng một đa diện có các mặt là những tam giác thì tổng số các mặt của nó là một số chẵn. Cho ví dụ. Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Gọi số mặt của đa diện \(H\) là \( m\), tìm số cạnh của đa diện. +) Số cạnh của đa diện là số nguyên, từ đó suy ra số mặt của đa diện là số chẵn. +) Lấy ví dụ: Tứ diện. Lời giải chi tiết Giả sử đa diện \((H)\) có \(m\) mặt. Vì mỗi mặt của \((H)\) có 3 cạnh, nên \(m\) mặt có \(3m\) cạnh. Nhưng mỗi cạnh của \((H)\) là cạnh chung của đúng hai mặt nên số cạnh của \((H)\) bằng \(c =\dfrac {3m} 2\). Do \(c\) là số nguyên dương nên \(m\) phải là số chẵn. Ví dụ: Tứ diện có các mặt đều là hình tam giác và số mặt của tứ diện bằng \(4\) là một số chẵn.
HocTot.XYZ
|