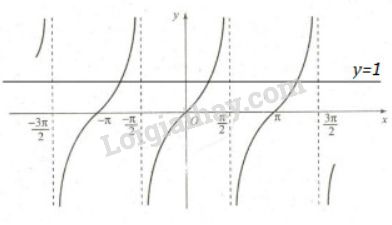
Giải bài 1 trang 17 SGK Đại số và Giải tích 11Hãy xác định các giá trị của x trên đoạn Video hướng dẫn giải Hãy xác định các giá trị của \(x\) trên đoạn \(\displaystyle\left[ { - \pi ;{{3\pi } \over 2}} \right]\) để hàm số \(y = \tan x\); LG a Nhận giá trị bằng \(0\); Phương pháp giải: B1: Vẽ đường thẳng y=0 (Ox) B2: Quan sát xem đồ thị hàm số cắt đường thẳng y=0 tại những điểm nào. B3: Chỉ lấy những điểm thuộc đoạn đã cho và KL. Lời giải chi tiết:
Trong đoạn \(\displaystyle\left[ { - \pi ;{{3\pi } \over 2}} \right]\), Trục hoành cắt đồ thị hàm số \(y = \tan x\) tại ba điểm có hoành độ \(- π ; 0 ; π\). Vậy \(x = - π; x = 0 ; x = π\). LG b Nhận giá trị bằng \(1\); Phương pháp giải: B1: Vẽ đường thẳng y=1 (Ox) B2: Quan sát xem đồ thị hàm số cắt đường thẳng y=1 tại những điểm nào. B3: Chỉ lấy những điểm thuộc đoạn đã cho và KL. Lời giải chi tiết: Đường thẳng \(y = 1\) cắt đồ thị \(y = \tan x\) tại ba điểm có hoành độ \(\displaystyle {\pi \over 4};{\pi \over 4} \pm \pi \). Vậy \(\displaystyle x = - {{3\pi } \over 4};\,\,x = {\pi \over 4};\,\,x = {{5\pi } \over 4}\). LG c Nhận giá trị dương; Phương pháp giải: B1: Quan sát đồ thị hàm số, tìm các giá trị x sao cho đồ thị nằm phía trên trục hoành (hay tanx >0). B2. Lấy các điểm thuộc đoạn đề bài yêu cầu và Kết luận. Lời giải chi tiết: Trong các khoảng \(\displaystyle\left( { - \pi ; - {\pi \over 2}} \right)\); \(\displaystyle\left( {0;{\pi \over 2}} \right)\); \(\displaystyle \left( {\pi ;{{3\pi } \over 2}} \right)\), đồ thị hàm số nằm phía trên trục hoành. Vậy \(\displaystyle x \in \left( { - \pi ; - {\pi \over 2}} \right) \cup \left( {0;{\pi \over 2}} \right) \cup \left( {\pi ;{{3\pi } \over 2}} \right)\) LG d Nhận giá trị âm. Phương pháp giải: Quan sát đồ thị hàm số, tìm các điểm thỏa mãn yêu cầu bài toán. Lời giải chi tiết: Trong các khoảng \(\displaystyle\left( { - {\pi \over 2};0} \right),\left( {{\pi \over 2};\pi } \right)\), đồ thị hàm số nằm phía dưới trục hoành. Vậy \(\displaystyle x \in \left( { - {\pi \over 2};0} \right) \cup \left( {{\pi \over 2};\pi } \right)\). HocTot.XYZ
|