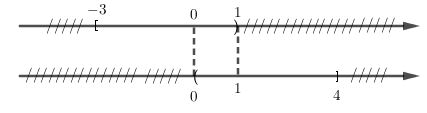
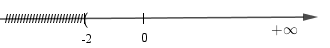Bài 1 trang 18 SGK Đại số 10Xác định các tập hợp sau và biểu diễn chúng trên trục số Video hướng dẫn giải Xác định các tập hợp sau và biểu diễn chúng trên trục số LG a \([-3;1) ∪ (0;4]\); Phương pháp giải: Hợp của hai tập hợp: Tập hợp C gồm các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B Lời giải chi tiết: \([-3;1) ∪ (0;4] = [-3; 4]\)
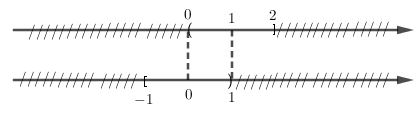
Chú ý: Để lấy được hợp hai tập hợp, các em biểu diễn riêng ra hai trục số (hai dòng) và lấy tất cả các phần: không bị gạch hoặc chỉ gạch ở một dòng. Ở hình vẽ trên, từ -3 đến 0 chỉ bị gạch 1 dòng, từ 0 đến 1 không bị gạch, từ 1 đến 4 cũng chỉ bị gạch 1 dòng nên khi lấy hợp ta lấy tất cả các khoảng này. Tại điểm -3, 0, 1, 4 cũng lấy được nên ta lấy hợp sẽ được kết quả [-3;4]. LG b \((0; 2] ∪ [-1;1)\); Lời giải chi tiết: \((0; 2] ∪ [-1;1) = [-1; 2]\)
Chú ý: Biểu diễn hai dòng: Từ -1 đến 0 chỉ gạch 1 dòng, từ 0 đến 1 không gạch, từ 1 đến 2 chỉ gạch 1 dòng nên ta lấy tất cả các khoảng này. Các điểm -1, 0, 1, 2 đều lấy được nên ta được kết quả [-1;2]. LG c \((-2; 15) ∪ (3; +∞)\); Lời giải chi tiết: \((-2; 15) ∪ (3; +∞) = (-2; +∞)\)
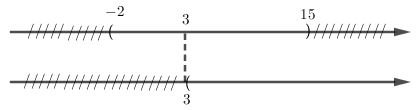
Chú ý: Biểu diễn hai dòng: Ta thấy từ -2 đến 3 chỉ bị gạch 1 dòng, từ 3 đến 15 không bị gạch, từ 15 đến \(+\infty\) bị gạch 1 dòng nên ta lấy tất cả các khoảng này. Các điểm 3, 15 lấy được, điểm -2 thì cả hai dòng đều không lấy nên không lấy điểm -2. Vậy ta được kết quả (-2; +∞). LG d \(\left(-1; {4 \over 3}\right) ∪ [-1; 2)\) Phương pháp giải: Hợp của hai tập hợp: Tập hợp C gồm các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B Lời giải chi tiết: \(\left(-1; {4 \over 3}\right) ∪ [-1; 2)=[-1;2)\)
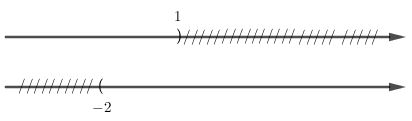
Cách khác: Ta thấy, \(\left( { - 1;\frac{4}{3}} \right) \subset \left[ { - 1;2} \right)\) nên \(\left(-1; {4 \over 3}\right) ∪ [-1; 2)=[-1;2)\). LG e \((-∞; 1) ∪ (-2; +∞)\). Phương pháp giải: Hợp của hai tập hợp: Tập hợp C gồm các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B Lời giải chi tiết: \((-∞; 1) ∪ (-2; +∞)=(-∞; +∞)\)
Chú ý: Biểu diễn hai dòng: Ta thấy từ \(-\infty\) đến -2 bị gạch 1 dòng, từ -2 đến 1 không bị gạch, từ 1 đến \(+\infty\) bị gạch 1 dòng nên ta lấy tất cả các khoảng này sẽ được kết quả R. HocTot.XYZ
|