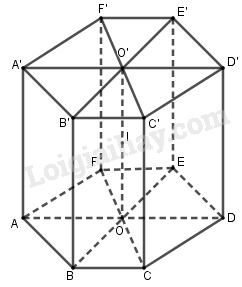
Bài 1 trang 99 SGK Hình học 12Cho lăng trụ lục giác đều ABCDEF.A'B'C'D'E'F' Đề bài Cho lăng trụ lục giác đều \(ABCDEF.A'B'C'D'E'F'\), \(O\) và \(O'\) là tâm đường tròn ngoại tiếp hai đáy, mặt phẳng \((P)\) đi qua trung điểm của \(OO'\) và cắt các cạnh bên của lăng trụ. Chứng minh rằng \((P)\) chia lăng trụ đã cho thành hai đa diện có thể tích bằng nhau. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào tính chất đối xứng tâm: Hai hình đối xứng nhau qua tâm I nào đó thì có thể tích bằng nhau. Lời giải chi tiết Gọi \(I\) là trung điểm của \(OO'\) thì \(I\) là tâm đối xứng của lăng trụ. ABCDEF.A'B'C'D'E'F' là hình lăng trụ lục giác đều nên I là tâm đối xứng của các hình chữ nhật ADD'A', BEE'B', CFF'C'. Vậy nếu mp(P) đi qua I và cắt các cạnh AA', BB', CC', DD', EE', FF' theo thứ tự tại các điểm M, N, P, Q, R, S thì I là trung điểm của MQ, NR và PS Suy ra phép đối xứng qua điểm I biến ABCDEF.MNPQRS thành D'E'F'A'B'C'.QRSMNP. Nghĩa là ABCDEF.MNPQRS và D'E'F'A'B'C'. QRSMNP là hai khối da điện bằng nhau. Vậy hai khối đa diện nói trên có thể tích bằng nhau. Nhận xét: Trong một hình bất kì trong không gian mà có tâm đối xứng, thì mặt phẳng đi qua tâm sẽ chia hình không gian đó thành hai phần có thể tích bằng nhau. HocTot.XYZ
|