Bài 12 trang 82 SGK Hình học 12 Nâng caoCho hình chóp S.ABC có đường cao SA = h, đáy là tam giác ABC vuông tại C, AC = b, BC = a. Gọi M là trung điểm của AC và N là điểm sao cho . a) Tính độ dài đoạn thẳng MN. b) Tìm sự liên hệ giữa a, b, h để MN vuông góc với SB.
Lựa chọn câu để xem lời giải nhanh hơn
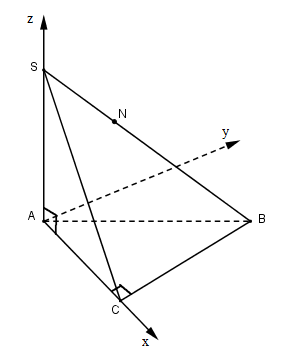
Cho hình chóp S.ABC có đường cao SA = h, đáy là tam giác ABC vuông tại C, AC = b, BC = a. Gọi M là trung điểm của AC và N là điểm sao cho \(\overrightarrow {SN} = {1 \over 3}\overrightarrow {SB} \). LG a Tính độ dài đoạn thẳng MN. Phương pháp giải: Chọn hệ trục Oxyz sao cho A trùng O, tia AC trùng tia Ox, AS trùng Oz. Tìm tọa độ các điểm và tính toán. Lời giải chi tiết:
Chọn hệ trục Oxyz như hình vẽ, B nằm trong góc xOy. \(M\left( {{b \over 2};0;0} \right),\overrightarrow {SB} = \left( {b;a; - h} \right)\) Gọi \(N\left( {x;y;z} \right)\) thì \(\overrightarrow {SN} = \left( {x;y;z - h} \right)\). \(\overrightarrow {SN} = {1 \over 3}\overrightarrow {SB} \Leftrightarrow \left\{ \matrix{ \(\eqalign{ LG b Tìm sự liên hệ giữa a, b, h để MN vuông góc với SB. Phương pháp giải: \(MN \bot SB \Leftrightarrow \overrightarrow {MN} .\overrightarrow {SB} = 0\) Lời giải chi tiết: \(MN \bot SB \Leftrightarrow \overrightarrow {MN} .\overrightarrow {SB} = 0\) \(\Leftrightarrow - {{{b^2}} \over 6} + {{{a^2}} \over 3} + {{ - 2{h^2}} \over 3} = 0 \) \(\Leftrightarrow 4{h^2} = 2{a^2} - {b^2}\) HocTot.XYZ
|