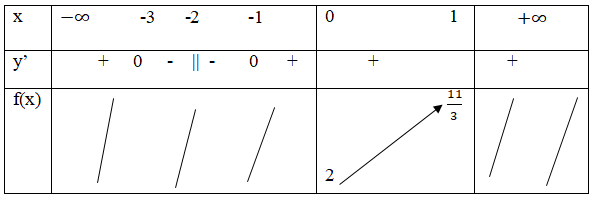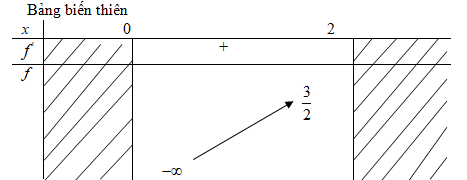Bài 17 trang 22 SGK Đại số và Giải tích 12 Nâng caoTìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
Lựa chọn câu để xem lời giải nhanh hơn
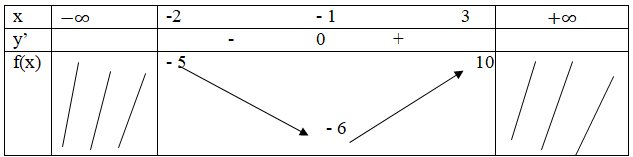
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: LG a \(f\left( x \right) = {x^2} + 2x - 5\) trên đoạn \(\left[ { - 2;3} \right]\); Lời giải chi tiết: \(D = \left[ { - 2;3} \right]\) \(f'\left( x \right) = 2x + 2\) \(f'\left( x \right) = 0 \Leftrightarrow x=- 1 \in \left[ { - 2;3} \right]\) Ta có: \(f\left( { - 2} \right) = - 5;f\left( { - 1} \right) = - 6;\) \(f\left( 3 \right) = 10\). Vậy: \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 2;3} \right]} = - 6;\mathop {\max \,f\left( x \right) = 10}\limits_{x \in \left[ { - 2;3} \right]} \). Cách khác: Hàm số f(x)= x2 + 2x – 5 Tập xác định D = R. Đạo hàm y’= 2x +2 = 0 ⇔ x = - 1 Bảng biến thiên:
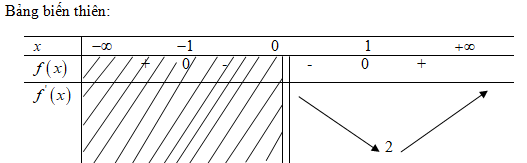
Vậy: \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 2;3} \right]} = - 6;\mathop {\max \,f\left( x \right) = 10}\limits_{x \in \left[ { - 2;3} \right]} \). LG b \(f\left( x \right) = {{{x^3}} \over 3} + 2{x^2} + 3x - 4\) trên đoạn \(\left[ { - 4;0} \right]\); Lời giải chi tiết: \(D = \left[ { - 4;0} \right]\) \(f'\left( x \right) = {x^2} + 4x + 3\) \(f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ Ta có: \(f\left( { - 4} \right) = - {{16} \over 3};f\left( { - 1} \right) = - {{16} \over 3};\) \(f\left( { - 3} \right) = - 4;f\left( 0 \right) = - 4\) Vậy \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 4;0} \right]} = - {{16} \over 3};\) \(\mathop {\max \,f\left( x \right)}\limits_{x \in \left[ { - 4;0} \right]} = - 4\). LG c \(f\left( x \right) = x + {1 \over x}\) trên đoạn \(\left( {0; + \infty } \right)\); Lời giải chi tiết: \(D = \left( {0; + \infty } \right)\) \(f'\left( x \right) = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}}\) với mọi \(x \ne 0\) \(f'\left( x \right) = 0 \Leftrightarrow x = \pm 1\) \(x=1\in \left( {0; + \infty } \right.)\) \(x=-1\not\in \left( {0; + \infty } \right.)\)
Vậy \(\mathop {\min \,\,f\left( x \right) = f\left( 1 \right)}\limits_{x \in \left( {0; + \infty } \right)} = 2\). Hàm số không đạt giá trị lớn nhất trên khoảng \(\left( {0; + \infty } \right)\). LG d \(f\left( x \right) = - {x^2} + 2x + 4\) trên đoạn \(\left[ {2;4} \right]\); Lời giải chi tiết: \(D = \left[ {2;4} \right]\) \(f'\left( x \right) = - 2x + 2\) \(f'\left( x \right) = 0 \Leftrightarrow x = 1 \notin \left[ {2;4} \right]\) Ta có: \(f\left( 2 \right) = 4;f\left( 4 \right) = - 4\) Vậy \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {2;4} \right]} = - 4;\) \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ {2;4} \right]} = 4\). LG e \(f\left( x \right) = {{2{x^2} + 5x + 4} \over {x + 2}}\) trên đoạn \(\left[ {0;1} \right]\); Lời giải chi tiết: \(D = \left[ {0;1} \right]\) \(f'\left( x \right) = {{2{x^2} + 8x + 6} \over {{{\left( {x + 2} \right)}^2}}}\) \(f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ Ta có: \(f\left( 0 \right) = 2;f\left( 1 \right) = {{11} \over 3}\) Vậy \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = 2;\) \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = {{11} \over 3}\) Cách khác: Bảng biến thiên:
Vậy \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = 2;\) \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = {{11} \over 3}\) LG f \(f\left( x \right) = x - {1 \over x}\) trên đoạn \(\left( {0;2} \right]\); Lời giải chi tiết: \(D = \left( {0;2} \right]\) \(f'\left( x \right) = 1 + {1 \over {{x^2}}} > 0\) với mọi \(x \in \left( {0;2} \right]\) \(f\left( 2 \right) = {3 \over 2}\)
Vậy \(\mathop {\,\max f\left( x \right)}\limits_{x \in \left[ {0;2} \right]} = {3 \over 2}\) . Hàm số không đạt giá trị nhỏ nhất trên \(\left( {0;2} \right]\). HocTot.XYZ
|