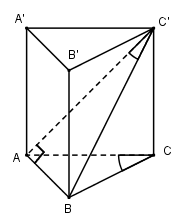
Bài 19 trang 28 SGK Hình học 12 Nâng caoCho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông tại A, AC = b. . Đường thẳng BC’ tạo với mp(AA’C’C) một góc . a) Tính độ dài đoạn thẳng AC. b) Tính thể tích khối lăng trụ đã cho.
Lựa chọn câu để xem lời giải nhanh hơn
Cho khối lăng trụ đứng \(ABC.A’B’C’\) có đáy là tam giác \(ABC\) vuông tại \(A, AC = b\). \(\widehat {ACB} = {60^0}\). Đường thẳng \(BC’\) tạo với mp \((AA’C’C)\) một góc \({30^0}\). LG a Tính độ dài đoạn thẳng \(AC'\). Phương pháp giải: - Góc giữa đường thẳng và mp bằng góc giữa đt và hình chiếu của nó trên mp. - Tính AC' dựa và tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết:
Ta có: \(BA \bot AC\) và \(BA \bot AA'\) nên \(BA \bot \left( {ACC'A'} \right)\) \(\Rightarrow AC' = AB.\cot{30^0} \) Tam giác ABC vuông tại A có \(AB= AC.\tan {60^0} \) \(= b\sqrt 3 \) Do đó \(\Rightarrow AC' = AB.\cot{30^0} \) \(= b\sqrt 3 .\sqrt 3=3b\) LG b Tính thể tích khối lăng trụ đã cho. Phương pháp giải: Thể tích lăng trụ V=Bh. Lời giải chi tiết: Trong tam giác vuông \(ACC’\), ta có: \(CC{'^2} = AC{'^2} - A{C^2} \) \(= 9{b^2} - {b^2} = 8{b^2} \) \(\Rightarrow CC' = 2\sqrt 2 b\) HocTot.XYZ
|