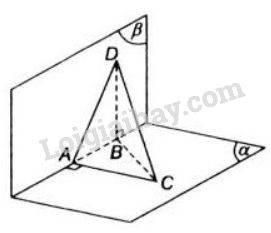
Bài 2 trang 113 SGK Hình học 11Cho hai mặt phẳng Đề bài Cho hai mặt phẳng \((\alpha)\) và \((\beta)\) vuông góc với nhau. Người ta lấy trên giao tuyến \(\Delta\) của hai mặt phẳng đó hai điểm \(A\) và \(B\) sao cho \(AB=8cm\). Gọi \(C\) là một điểm trên \((\alpha)\) và \(D\) là một điểm trên \((\beta)\) sao cho \(AC\) và \(BD\) cùng vuông góc với giao tuyến \(\Delta\) và \(AC=6cm\), \(BD=24cm\). Tính độ dài đoạn \(CD\). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Chứng minh \(AC\bot AD\) và sử dụng định lý Pi-ta-go để tính toán. Lời giải chi tiết
\(\left. \matrix{(\alpha ) \bot (\beta ) \hfill \cr AC \bot \Delta \hfill \cr AC \subset (\alpha ) \hfill \cr} \right\} \Rightarrow AC \bot (\beta )\) Do đó \(AC\bot AD\) hay tam giác \(ACD\) vuông tại \(A\) Áp dụng định lí Pytago vào tam giác \(ACD\) ta được: \(D{C^2} = A{C^2} + A{D^2}(1)\) Vì \(BD\bot AB \Rightarrow \Delta ABD\) vuông tại \(B\). Áp dụng định lí Pytago vào tam giác \(ABD\) ta được: \(A{D^2} = A{B^2} + B{D^2}(2)\) Từ (1) và (2) suy ra: \(D{C^2} = A{C^2} + A{B^2} + B{D^2} = {6^2} + {8^2} + {24^2} = 676\) \( \Rightarrow DC = \sqrt {676} = 26cm\) HocTot.XYZ
|