Bài 2 trang 122 SGK Hình học 12 Nâng caoCho tứ diện ABCD có thể tích V. Hãy tính thể tích hình tứ diện có đỉnh là trọng tâm các mặt của tứ diện đã cho. Đề bài Cho tứ diện ABCD có thể tích V. Hãy tính thể tích hình tứ diện có đỉnh là trọng tâm các mặt của tứ diện đã cho. Lời giải chi tiết
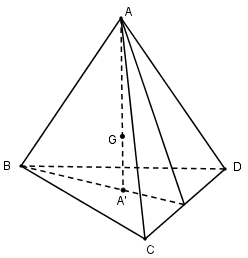
Gọi G là trọng tâm tứ diện ABCD và A’, B’, C’, D’ lần lượt là trọng tâm các tam giác BCD, ACD, ABD, ABC. Gọi \(V\left( {G; - {1 \over 3}} \right)\) là phép vị tự tâm G tỉ số \(k = - {1 \over 3}.\) Ta có: \(\overrightarrow {GA'} = - {1 \over 3}\overrightarrow {GA} .\) Suy ra: \(V\left( {G; - {1 \over 3}} \right):A \to A'.\) Tương tự: \(B \to B'\) \(\eqalign{ Do đó: \(V:ABCD \to A'B'C'D'.\) Vậy \({V_{A'B'C'D'}} = {\left| k \right|^3}{V_{ABCD}} = {1 \over {27}}V.\) HocTot.XYZ
|