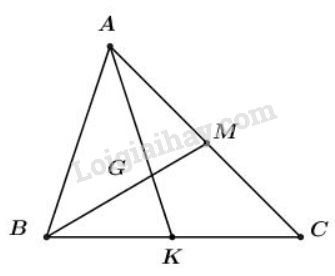
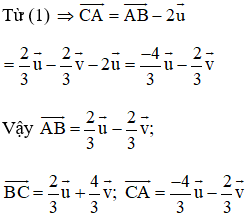Bài 2 trang 17 SGK Hình học 10Cho AK và BM là hai trung tuyến của tam giác ABC Đề bài Cho \(AK\) và \(BM\) là hai trung tuyến của tam giác \(ABC\). Hãy phân tích các vectơ \(\overrightarrow {AB} ,\overrightarrow {BC} ,\overrightarrow {CA} \) theo hai vectơ sau \(\overrightarrow u = \overrightarrow {AK} ,\overrightarrow v = \overrightarrow {BM} .\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Sử dụng tính chất của đường trung tuyến. +) Với 3 điểm \(A, \, \, B, \, \, C\) bất kì ta luôn có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} .\) Lời giải chi tiết Gọi \(G\) là giao điểm của \(AK, BM\) thì \(G\) là trọng tâm của tam giác. Áp dụng tính chất đường trung tuyến của tam giác ta có: \(\eqalign{ Theo quy tắc \(3\) điểm đối với tổng vec tơ: \(\overrightarrow {AB} = \overrightarrow {AG} + \overrightarrow {GB}\)\( \Rightarrow \overrightarrow {AB} = {2 \over 3}\overrightarrow u - {2 \over 3}\overrightarrow v \) \(AK\) là trung tuyến nên K là trung điểm \(BC\). Do đó, \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AK} \)\( \Rightarrow ({2 \over 3}\overrightarrow u - {2 \over 3}\overrightarrow v) + \overrightarrow {AC} = 2\overrightarrow u \) \(\Rightarrow \overrightarrow {AC} = 2\overrightarrow u - \dfrac{2}{3}\overrightarrow u + \dfrac{2}{3}\overrightarrow v \) \( \Rightarrow \overrightarrow {AC} = {4 \over 3}\overrightarrow u + {2 \over 3}\overrightarrow v \)\( \Rightarrow \overrightarrow {CA} = - {4 \over 3}\overrightarrow u - {2 \over 3}\overrightarrow v \) \(BM\) là trung tuyến nên \(M\) là trung điểm \(AC\). Do đó, \(\eqalign{ Cách khác: + K là trung điểm của BC nên ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AK} \) hay \(\overrightarrow {AB} - \overrightarrow {CA} = 2\overrightarrow u \,\,\left( 1 \right)\) + M là trung điểm AC nên ta có: \(\overrightarrow {BA} + \overrightarrow {BC} = 2\overrightarrow {BM} \) hay \( - \overrightarrow {AB} + \overrightarrow {BC} = 2\overrightarrow v \,\,\left( 2 \right)\) + Lại có \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow 0 \,\,\left( 3 \right)\) Cộng (1) với (3) ta được \(2\overrightarrow {AB} + \overrightarrow {BC} = 2\overrightarrow u \), kết hợp với (2) ta được hệ phương trình: \(\left\{ \begin{array}{l}2\overrightarrow {AB} + \overrightarrow {BC} = 2\overrightarrow u \\ - \overrightarrow {AB} + \overrightarrow {BC} = 2\overrightarrow v \end{array} \right.\) Trừ hai vế của hai pt cho nhau ta được: \(3\overrightarrow {AB} = 2\overrightarrow u - 2\overrightarrow v \Leftrightarrow \overrightarrow {AB} = \frac{2}{3}\overrightarrow u - \frac{2}{3}\overrightarrow v \) \(\begin{array}{l} \Rightarrow - \left( {\frac{2}{3}\overrightarrow u - \frac{2}{3}\overrightarrow v } \right) + \overrightarrow {BC} = 2\overrightarrow v \\ \Leftrightarrow \overrightarrow {BC} = 2\overrightarrow v + \frac{2}{3}\overrightarrow u - \frac{2}{3}\overrightarrow v \\ \Rightarrow \overrightarrow {BC} = \frac{2}{3}\overrightarrow u + \frac{4}{3}\overrightarrow v \end{array}\)
HocTot.XYZ
|