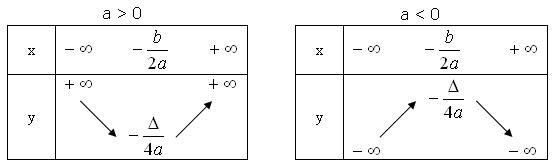
Bài 2 trang 49 SGK Đại số 10Lập bảng biến thiên và vẽ đồ thị của các hàm số. Video hướng dẫn giải Lập bảng biến thiên và vẽ đồ thị của các hàm số. LG a \(y = 3x^2- 4x + 1\); Phương pháp giải: Dựa vào đồ thị của hàm số \(y= a x^2 + bx + c\) ( \(a \ne 0\)), ta có bảng biến thiên của nó trong hai trường hợp \(a > 0\) và \(a < 0\) như sau:
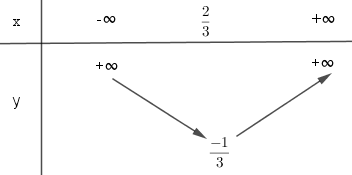
Cách vẽ: Bước 1: Xác định tọa độ của đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\) Bước 2: Vẽ trục đối xứng \(x = - \frac{b}{{2a}}\) Bước 3: Xác định tọa độ các giao điểm của parabol với trục tung, trục hoành ( nếu có) Xác định thêm một số điểm thuộc đồ thị để vẽ đồ thị chính xác hơn. 4) Vẽ parabol Khi vẽ parabol cần lưu ý đến dấu của hệ số \(a (a > 0\) thì bề lõm quay lên trên\(); (a < 0\) thì bề lõm quay xuống dưới). Lời giải chi tiết: \(y = 3x^2- 4x + 1\) Bảng biến thiên:
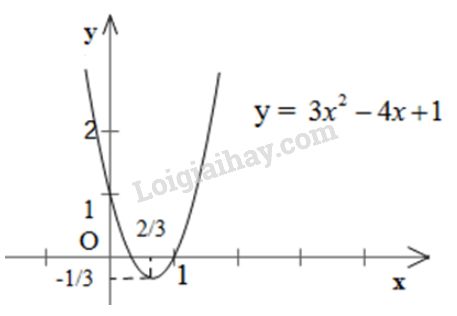
Đồ thị: - Đỉnh: \(I\left( {{2 \over 3}; - {1 \over 3}} \right)\) - Trục đối xứng: \(x = {2 \over 3}\) - Giao điểm với trục tung \(A(0; 1)\) - Giao điểm với trục hoành \(B\left( {{1 \over 3};0} \right)\), \(C(1; 0)\).
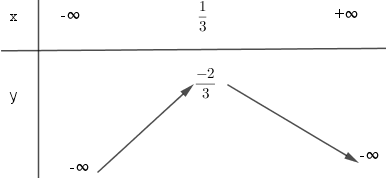
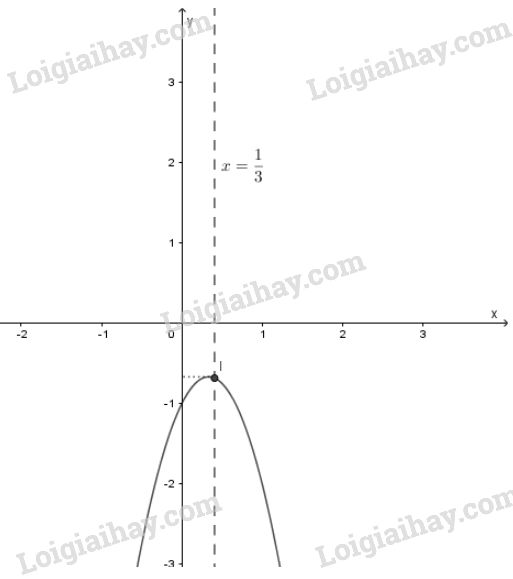
LG b \(y = - 3x^2+ 2x – 1\); Lời giải chi tiết: \(y = - 3x^2+ 2x – 1\) Bảng biến thiên:
Vẽ đồ thị: - Đỉnh \(I\left( {{1 \over 3}; - {2 \over 3}} \right)\), trục đối xứng: \(x = {1 \over 3}\) - Giao điểm với trục tung \(A(0;- 1)\). - Giao điểm với trục hoành: không có. Ta xác định thêm điểm phụ: \(B(1;- 2)\), \(C(-1;- 6)\).
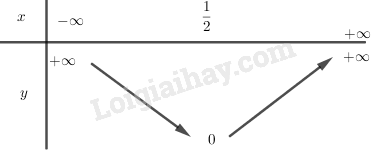
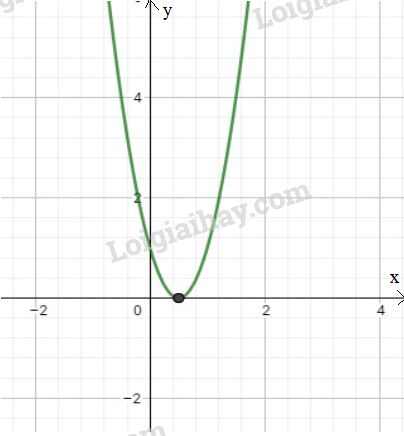
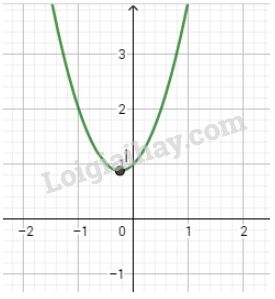
LG c \(y = 4x^2- 4x + 1\); Lời giải chi tiết: \(y = 4x^2- 4x + 1\). Lập bảng biến thiên: Đồ thị: + Đỉnh \(I\left( {\dfrac{1}{2};0} \right)\), trục đối xứng \(x=\dfrac{1}{2}\) + Tiếp xúc với trục \(Ox\) tại \(I\). + Cắt trục \(Oy\) tại \(A(0;1)\). + Cắt trục \(Ox\) tại \(B(\dfrac{1}{2};0)\).
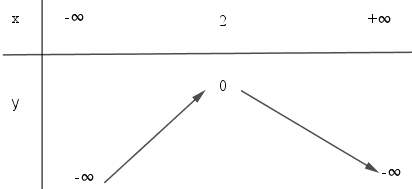
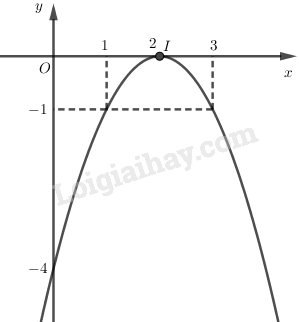
LG d \(y = - x^2+ 4x – 4\); Lời giải chi tiết: \(y = - x^2+ 4x – 4\) Bảng biến thiên:
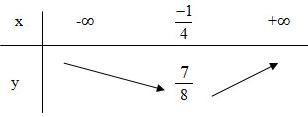
Đồ thị: + Đỉnh \(I(2;0)\), trục đối xứng \(x=2\). + Tiếp xúc với trục \(Ox\) tại \(I\). + Cắt \(Oy\) tại \(A(0;-4)\). + Lấy thêm hai điểm phụ \((1;-1)\) và \((3;-1)\). LG e \(y = 2x^2+ x + 1\); Lời giải chi tiết: \(y = 2x^2+ x + 1\); - Đỉnh \(I\left( {{{ - 1} \over 4};{{ 7} \over 8}} \right)\) - Trục đối xứng: \(x = {{ - 1} \over 4}\) - Giao \(Ox\): Đồ thị không giao với trục hoành - Giao \(Oy\): Giao với trục tung tại điểm \((0;1)\) Bảng biến thiên: Vẽ đồ thị theo bảng sau:
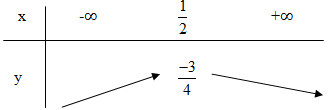
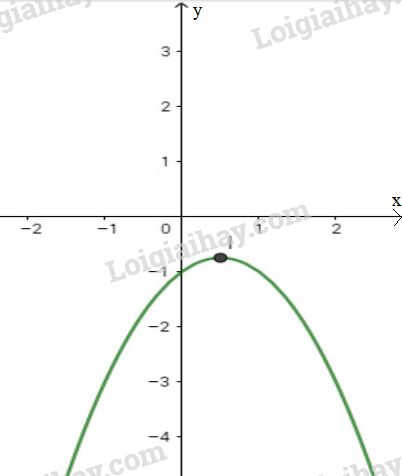
LG f \(y = - x^2+ x - 1\). Lời giải chi tiết: \(y = - x^2+ x - 1\). - Đỉnh \(I\left( {{1 \over 2};{{ - 3} \over 4}} \right)\) - Trục đối xứng: \(x = {1 \over 2}\) - Giao \(Ox\): Đồ thị không giao với trục hoành - Giao \(Oy\): Giao với trục tung tại điểm \((0;-1)\) Bảng biến thiên:
Vẽ đồ thị theo bảng sau:
HocTot.XYZ
|