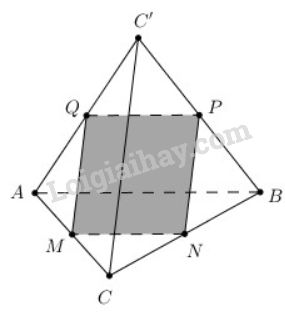
Bài 4 trang 98 SGK Hình học 11Trong không gian cho hai tam giác đều ABC và A'B'C'... Đề bài Trong không gian cho hai tam giác đều \(ABC\) và \(ABC'\) có chung cạnh \(AB\) và nằm trong hai mặt phẳng khác nhau. Gọi \(M, N, P, Q\) lần lượt là trung điểm của các cạnh \(AC, CB, BC', C'A,\) Chứng minh rắng: a) \(AB ⊥ CC'\); b) Tứ giác \(MNPQ\) là hình chữ nhật. Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Chứng minh \(\overrightarrow {AB} .\overrightarrow {CC'} = 0\). b) Dựa vào tính chất của đường trung bình của tam giác, chứng minh \(MNPQ\) là hình bình hành, từ đó chứng minh \(MNPQ\) là hình chữ nhật. Lời giải chi tiết
a) \(\overrightarrow{AB}.\overrightarrow{CC'}=\overrightarrow{AB}.(\overrightarrow{AC'}-\overrightarrow{AC})\) \(=\overrightarrow{AB}.\overrightarrow{AC'}-\overrightarrow{AB}.\overrightarrow{AC}\) \(=AB.AC'.\cos \widehat {BAC'}-AB.AC.\cos\widehat {BAC}\) \( = a.a.\dfrac{1}{2} - a.a.\dfrac{1}{2} = 0\) \(\Rightarrow AB ⊥ CC'\). b) Theo giả thiết \(Q,P\) là trung điểm của \(AC',BC'\) do đó \(QP\) là đường trung bình của tam giác \(ABC'\) Suy ra: \(QP//AB,QP={1\over 2}AB\) (1) Chứng minh tương tự ta có: \(PN//CC',PN={1\over 2}CC'\) \(MN//AB,MN={1\over 2}AB\) (2) Từ (1) và (2) suy ra: \(MN//QP,MN=QP\). Do đó \(MNPQ\) là hình bình hành. Ta có: \(MN//AB\), \(PN//CC'\) mà \(AB\bot CC'\) do đó \(MN\bot NP\) Hình bình hành \(MNPQ\) có một góc vuông nên \(MNPQ\) là hình chữ nhật. HocTot.XYZ
|