Bài 41 trang 44 SGK giải tích 12 nâng caoa) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: b) Tùy theo các giá trị của m, hãy biện luận số nghiệm của phương trình:
Lựa chọn câu để xem lời giải nhanh hơn
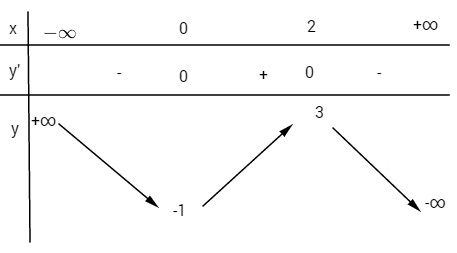
LG a Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = - {x^3} + 3{x^2} - 1\). Lời giải chi tiết: TXĐ: \(D =\mathbb R\) \(\eqalign{ Bảng biến thiên:
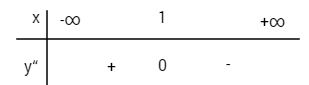
Hàm đồng biến trên khoảng \((0;2)\), nghịch biến trên mỗi khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\). Hàm số đạt cực tiểu tại điểm \(x = 0\), giá trị cực tiểu \(y(0) = -1\). Hàm số đạt cực đại tại điểm \(x = 2\), giá trị cực đại \(y(2) = 3\). Đồ thị: \(y'' = - 6x + 6\) \(y'' = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = 1\) Xét dấu y”:
\(I(1;1)\) là điểm uốn của đồ thị Điểm đặc biệt: \(x = 0 \Rightarrow y = - 1\) \(x = - 1 \Rightarrow y = 3\)
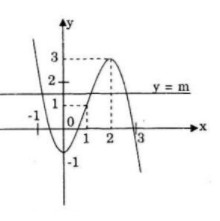
LG b Tùy theo các giá trị của \(m\), hãy biện luận số nghiệm của phương trình: \( - {x^3} + 3{x^2} - 1 = m\) Lời giải chi tiết: Số nghiệm của phương trình chính là số giao điểm của đồ thị \((C)\) hàm số \(y = - {x^3} + 3{x^2} - 1\) với đường thẳng \(y = m\) cùng phương với trục \(Ox\). Dựa vào đồ thị ở câu a) ta có: - Nếu m > 3: Phương trình (*) có 1 nghiệm - Nếu m = 3: Phương trình (*) có 2 nghiệm. - Nếu -1 < m < 3 : Phương trình (*) có 3 nghiệm - Nếu m = -1: Phương trình (*) có 2 nghiệm. - Nếu m < -1 phương trình (*) có 1 nghiệm. Vậy, - Nếu \(m < -1\) hoặc \(m > 3\) thì phương trình có \(1\) nghiệm; - Nếu \(m = -1\) hoặc \(m = 3\) thì phương trình có \(2\) nghiệm; - Nếu \(-1 < m < 3\) thì phương trình có \(3\) nghiệm. HocTot.XYZ
|