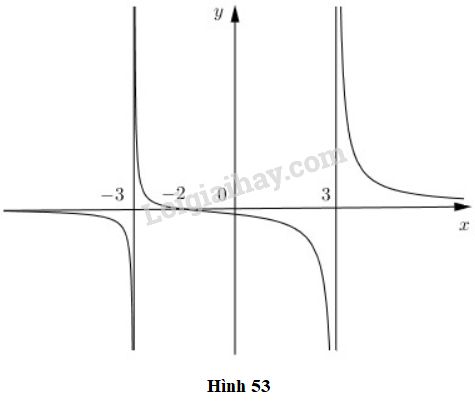
Bài 5 trang 133 SGK Đại số và Giải tích 11Cho hàm số Video hướng dẫn giải Cho hàm số \(f(x) = \dfrac{x+2}{x^{2}-9}\) có đồ thị như trên hình 53.
LG a Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi \(x → -∞\), \(x → 3^-\) và \(x → -3^+\) Phương pháp giải: Quan sát đồ thị hàm số. Lời giải chi tiết: Quan sát đồ thị ta thấy \(x → -∞\) thì \(f(x) → 0\); khi \(x → 3^-\) thì \(f(x) → -∞\); khi \(x → -3^+\) thì \(f(x) → +∞\). LG b Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau: \(\underset{x\rightarrow -\infty }{\lim} f(x)\) với \(f(x)\) được xét trên khoảng \((-\infty; -3)\), \(\underset{x\rightarrow 3^{-}}{\lim} f(x)\) với \(f(x)\) được xét trên khoảng \((-3,3)\), \(\underset{x\rightarrow -3^{+}}{\lim} f(x)\) với \(f(x)\) được xét trên khoảng \((-3; 3)\). Phương pháp giải: Tính các giới hạn, sử dụng quy tắc tính giới hạn được học và kết luận. Lời giải chi tiết: +) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) \) \(= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{x + 2}}{{{x^2} - 9}} \) \(= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{x\left( {1 + \dfrac{2}{x}} \right)}}{{x\left( {x - \dfrac{9}{x}} \right)}}\) \( = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{1 + \dfrac{2}{x}}}{{x - \dfrac{9}{x}}}\) Mà \({\mathop {\lim }\limits_{x \to - \infty } \left( {1 + \dfrac{2}{x}} \right) = 1}\) và \({\mathop {\lim }\limits_{x \to - \infty } \left( {x - \dfrac{9}{x}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {x\left( {1 - \dfrac{9}{{{x^2}}}} \right)} \right] = - \infty }\) nên \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) \)\(=0\) +) \(\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{x + 2}}{{{x^2} - 9}}\) Vì \(\mathop {\lim }\limits_{x \to {3^ - }} \left( {x + 2} \right) = 3 + 2 = 5 > 0\) và \(\mathop {\lim }\limits_{x \to {3^ - }} \left( {{x^2} - 9} \right) = 0\); \({x^2} - 9 < 0\) khi \(x<3\) nên \(\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right)=-\infty \). +) \(\mathop {\lim }\limits_{x \to {(-3)^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {(-3)^ + }} \dfrac{{x + 2}}{{{x^2} - 9}}\) Vì \(\mathop {\lim }\limits_{x \to {(-3)^ + }} \left( {x + 2} \right) = -3 + 2 = -1 < 0\) và \(\mathop {\lim }\limits_{x \to {(-3)^ + }} \left( {{x^2} - 9} \right) = 0\); \({x^2} - 9 < 0\) khi \(x>-3\) nên \(\mathop {\lim }\limits_{x \to {(-3)^ + }} f\left( x \right)=+\infty \). Cách khác: \(\underset{x\rightarrow -\infty }{\lim} f(x) = \underset{x\rightarrow -\infty }{\lim}\) \(\dfrac{x+2}{x^{2}-9}\) = \(\underset{x\rightarrow -\infty }{\lim}\) \(\dfrac{\dfrac{1}{x}+\dfrac{2}{x^{2}}}{1-\dfrac{9}{x^{2}}} = 0\). \(\underset{x\rightarrow 3^{-}}{\lim} f(x) = \underset{x\rightarrow 3^{-}}{\lim}\)\(\dfrac{x+2}{x^{2}-9}\) = \(\underset{x\rightarrow 3^{-}}{\lim}\) \(\dfrac{x+2}{x+3}.\dfrac{1}{x-3} = -∞ \) vì \(\underset{x\rightarrow 3^{-}}{\lim}\)\(\dfrac{x+2}{x+3}\) = \(\dfrac{5}{6} > 0\) và \(\underset{x\rightarrow 3^{-}}{\lim} \dfrac{1}{x-3} = -∞\). \(\underset{x\rightarrow -3^{+}}{\lim} f(x) =\) \(\underset{x\rightarrow -3^{+}}{\lim}\) \(\dfrac{x+2}{x^{2}-9}\) = \(\underset{x\rightarrow -3^{+}}{\lim}\) \(\dfrac{x+2}{x-3}\) . \(\dfrac{1}{x+3} = +∞\) vì \(\underset{x\rightarrow -3^{+}}{\lim}\) \(\dfrac{x+2}{x-3}\) = \(\dfrac{-1}{-6}\) = \(\dfrac{1}{6} > 0\) và \(\underset{x\rightarrow -3^{+}}{\lim}\) \(\dfrac{1}{x+3} = +∞\). HocTot.XYZ
|