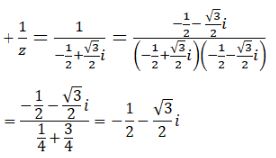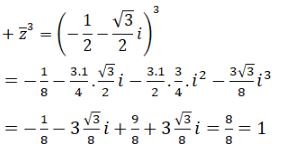Bài 5 trang 190 SGK Đại số và Giải tích 12 Nâng caoHãy tính Đề bài Cho \(z = - {1 \over 2} + {{\sqrt 3 } \over 2}i.\) Hãy tính \({1 \over z}\); \(\overline z \); \({z^2}\); \({\left( {\overline z } \right)^3}\); \(1 + z + {z^2}\). Phương pháp giải - Xem chi tiết Sử dụng các công thức: \(\dfrac{1}{z} = \dfrac{{\overline z }}{{{{\left| z \right|}^2}}}\) Kết hợp các công thức cộng, trừ nhân số phức. Lời giải chi tiết Ta có \(z = - \frac{1}{2} + \frac{{\sqrt 3 }}{2}i \) \(\Rightarrow \overline z = - \frac{1}{2} - \frac{{\sqrt 3 }}{2}i\) \(\left| z \right| = \sqrt {{{\left( { - {1 \over 2}} \right)}^2} + {{\left( {{{\sqrt 3 } \over 2}} \right)}^2}} = 1\) Nên \({1 \over z} = {{\overline z } \over {{{\left| z \right|}^2}}} = \overline z = - {1 \over 2} - {{\sqrt 3 } \over 2}i\) \({z^2} = {\left( { - {1 \over 2} + {{\sqrt 3 } \over 2}i} \right)^2} \) \(= {1 \over 4} - {{\sqrt 3 } \over 2}i - {3 \over 4} = - {1 \over 2} - {{\sqrt 3 } \over 2}i\) \(\begin{array}{l} \(1 + z + {z^2}\) \( = 1 + \left( { - {1 \over 2} + {{\sqrt 3 } \over 2}i} \right) + \left( { - {1 \over 2} - {{\sqrt 3 } \over 2}i} \right)\) \( = 0\) Chú ý: Có thể tính \(\frac{1}{z}\) và \(\left( {\overline z } \right)^3\) như sau: HocTot.XYZ
|