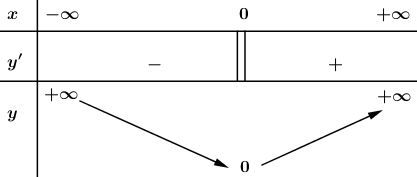
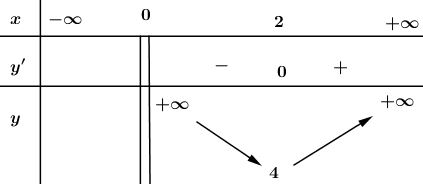
Giải bài 5 trang 24 SGK Giải tích 12Tính giá trị nhỏ nhất của các hàm số sau: Video hướng dẫn giải LG a Tính giá trị nhỏ nhất của các hàm số sau: \(y =|x|\) ; Phương pháp giải: - Phá dấu giá trị tuyệt đối đưa hàm số về dạng khoảng. - Lập bảng biến thiên và kết luận. Lời giải chi tiết: \(y=\left| x \right|.\) Ta có: \(y = |x| = \left\{ \begin{gathered} Tập xác định: \(D=\mathbb R.\) \(y' = \left\{ \begin{array}{l} Ta có bảng biến thiên: Từ bảng biến thiên ta có hàm số đạt GTNN tại \(x=0;{\min }\,y=0.\) LG b \(\displaystyle y =x+{4\over x}\) \(\displaystyle ( x > 0)\). Phương pháp giải: - Tìm TXĐ. - Tính đạo hàm và tìm nghiệm. - Lập bảng biến thiên rồi kết luận. Lời giải chi tiết: \(y=x+\dfrac{4}{x}\ \ \ \left( x>0 \right).\) Ta có: \(y'=1-\dfrac{4}{{{x}^{2}}}\) \(\Rightarrow y'=0\Leftrightarrow 1-\dfrac{4}{{{x}^{2}}}=0\) \(\Leftrightarrow {{x}^{2}}-4=0\Leftrightarrow \left[ \begin{align}& x=-2\notin \left( 0;+\infty \right) \\ & x=2\in \left( 0;+\infty \right) \\ \end{align} \right.\) Bảng biến thiên: Từ bảng biến thiên ta thấy: \(\underset{\left( 0;+\infty \right)}{\mathop{min}}\,y=4\ \ khi\ \ x=2.\) Cách khác: Áp dụng BĐT Cô-si ta có: \(y = x + \dfrac{4}{x} \ge 2\sqrt {x.\dfrac{4}{x}} = 4 \) \(\Rightarrow y \ge 4 \) \(\Rightarrow \mathop {\min }\limits_{\left( {0; + \infty } \right)} y = 4\) khi \(x = \dfrac{4}{x} \Leftrightarrow {x^2} = 4 \Leftrightarrow x = 2\). HocTot.XYZ
|