Bài 5 trang 83 SGK Đại số và Giải tích 11Chứng minh rằng Đề bài Chứng minh rằng số đường chéo của một đa giác lồi \(n\) cạnh là \(\displaystyle {{n(n - 3)} \over 2}\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Ta chứng minh khẳng định đúng với mọi \(n \in{\mathbb N}^*\), \(n ≥ 4\). Sử dụng phương pháp quy nạp toán học để chứng minh. Lời giải chi tiết Kí hiệu số đường chéo của đa giác \(n\) cạnh là \(C_n\). Ta chứng minh \(\displaystyle C_n = {{n(n - 3)} \over 2}\) (1) với mọi \(n \in{\mathbb N}^*\), \(n ≥ 4\). *) Với \(n = 4\), ta có tứ giác nên nó có 2 đường chéo. Mặt khác \(\displaystyle {{4(4 - 3)} \over 2} = 2\) nên (1) đúng với \(n = 4\). Vậy khẳng định đúng với \(n= 4\). *) Giả sử (1) đúng với \(n = k ≥ 4\), tức là \(C_k = \displaystyle {{k(k - 3)} \over 2}\) *) Ta phải chứng minh (1) đúng với \(n = k + 1\).
Tức là \(C_{k+1}=\displaystyle {{(k + 1)((k + 1) - 3)} \over 2}\)
Xét đa giác lồi \(k + 1\) cạnh
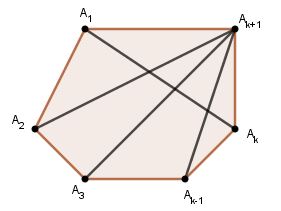 Đa giác \(k\) cạnh \(A_1A_2...A_k\) có \(\displaystyle {{k(k - 3)} \over 2}\) đường chéo (giả thiết quy nạp).
Nối \(A_{k+1}\) với các đỉnh \(A_2,...,A_{k-1}\), ta được thêm \(k -2\) đường chéo.
Ngoài ra \(A_1A_k\) cũng là một đường chéo.
Vậy số đường chéo của đa giác \(k + 1\) cạnh là \(\displaystyle {{k(k - 3)} \over 2}+ k - 2 + 1\) \( = \dfrac{{{k^2} - 3k}}{2} + k - 1 \) \(= \dfrac{{{k^2} - 3k + 2k - 2}}{2}\) \(\displaystyle ={{{k^2} - k - 2} \over 2} \) \( = \dfrac{{\left( {k + 1} \right)\left( {k - 2} \right)}}{2}\) \(\displaystyle = {{(k + 1)((k + 1) - 3)} \over 2}\) Như vậy, khẳng định cũng đúng với đa giác \(k + 1\) cạnh Vậy bài toán đã được chứng minh. Chú ý: Trên đây là cách chứng minh bằng quy nạp, các em có thể dễ dàng chứng minhcông thức đó bằng kiến thức chương 2 như sau: Cách 2: Đa giác lồi \(n\) cạnh có \(n\) đỉnh. Chọn 2 điểm bất kì trong số các đỉnh của một đa giác ta được 1 cạnh hoặc 1 đường chéo của đa giác. ⇒ Tổng số cạnh và đường chéo của đa giác bằng: \(C_n^2 = \dfrac{{n!}}{{2!\left( {n - 2} \right)!}}\)\( = \dfrac{{n\left( {n - 1} \right)\left( {n - 2} \right)!}}{{2\left( {n - 2} \right)!}} = \dfrac{{n\left( {n - 1} \right)}}{2}\) ⇒ Số đường chéo của đa giác lồi có \(n\) cạnh là: \(\dfrac{{n\left( {n - 1} \right)}}{2} - n = \dfrac{{{n^2} - n - 2n}}{2}\)\( = \dfrac{{{n^2} - 3n}}{2} = \dfrac{{n\left( {n - 3} \right)}}{2}\) Vậy ta có đpcm. HocTot.XYZ
|













