Bài 52 Trang 177 SGK Đại số và Giải tích 12 Nâng caoTính diện tích của các hình phẳng giới hạn bởi:
Lựa chọn câu để xem lời giải nhanh hơn
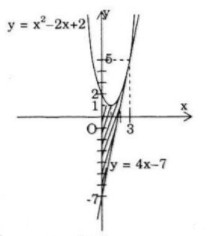
Tính diện tích của các hình phẳng giới hạn bởi: LG a Parabol \(y = {x^2} - 2x + 2,\) tiếp tuyến của nó tại điểm \(M(3;5)\) và trục tung Phương pháp giải: - Viết phương trình tiếp tuyến. - Dựng hình suy ra công thức tính diện tích. Lời giải chi tiết:
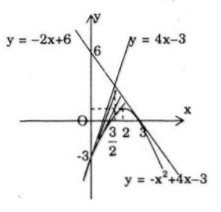
Ta có \(y' = 2x - 2 \Rightarrow y'\left( 3 \right) = 4.\) \(\eqalign{ LG b Parabol \(y = - {x^2} + 4x - 3\) và các tiếp tuyến của nó tại các điểm \(A(0;-3)\) và \(B(3;0)\) Phương pháp giải: - Viết phương trình tiếp tuyến. - Dựng hình suy ra công thức tính diện tích. Lời giải chi tiết:
Ta có \(y' = - 2x + 4 \) \(\Rightarrow y'\left( 0 \right) = 4;y'\left( 3 \right) = - 2\) Kí hiệu \({A_1}\) và \({A_2}\) là tam giác cong \(ACD\) Và \(BCD\). Ta có : \(S\left( {{A_1}} \right) = \int\limits_0^{{3 \over 2}} {\left( {4x - 3 + {x^2} - 4x + 3} \right)} dx \) \(= \int\limits_0^{{3 \over 2}} {{x^2}dx = \left. {{{{x^3}} \over 3}} \right|_0^{{3 \over 2}}} = {9 \over 8}\) \(S\left( {{A_2}} \right) = \int\limits_{{3 \over 2}}^3 {\left( { - 2x + 6 + {x^2} - 4x + 3} \right)} dx \) \(= \int\limits_{{3 \over 2}}^3 {{{\left( {x - 3} \right)}^2}dx = } \left. {{1 \over 3}{{\left( {x - 3} \right)}^3}} \right|_{{3 \over 2}}^3 = {9 \over 8}\) Vậy \(S = S\left( {{A_1}} \right) + S\left( {{A_2}} \right) = {9 \over 8} + {9 \over 8} = {9 \over 4}\) HocTot.XYZ
|