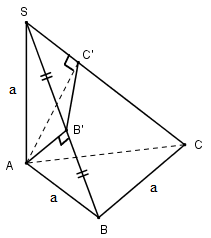
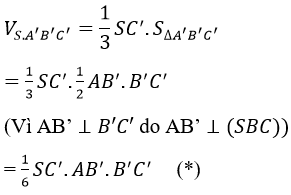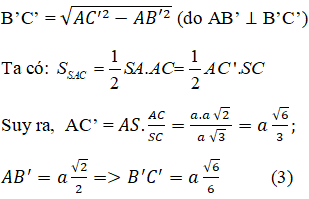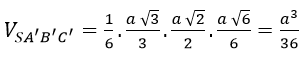Bài 6 trang 31 SGK Hình học 12 Nâng caoCho khối chóp S.ABC cố đường cao S/4 bằng a, đáy là tam giác vuông cân có AB = BC = a. Gọi B' là trung điểm của SB, C' là chân đường cao hạ từ A của tam giác SAC. a) Tính thể tích khối chóp S.ABC. b) Chứng minh rằng sc vuông góc với mp(AB'C'). c) Tính thể tích khối chóp S.AB’C’.
Lựa chọn câu để xem lời giải nhanh hơn
Cho khối chóp \(S.ABC\) có đường cao \(SA\) bằng \(a\), đáy là tam giác vuông cân có \(AB = BC = a\). Gọi \(B'\) là trung điểm của \(SB, C'\) là chân đường cao hạ từ \(A\) của tam giác \(SAC\). LG a Tính thể tích khối chóp \(S.ABC\). Lời giải chi tiết:
Tam giác ABC vuông cân tại B nên \({S_{ABC}} = \frac{1}{2}AB.BC = \frac{1}{2}a.a = \frac{{{a^2}}}{2}\) Thể tích khối chóp \(S.ABC\) là: \({V_{S.ABC}} = {1 \over 3}{S_{ABC}}.SA = {1 \over 3}.\frac{{{a^2}}}{2} .a = {{{a^3}} \over 6}\) LG b Chứng minh rằng \(SC\) vuông góc với mp \((AB'C')\). Lời giải chi tiết: Ta có \(BC \bot BA\) và \(BC \bot SA\) nên \(BC \bot \left( {SAB} \right)\) Mà \(AB' \subset \left( {SAB} \right)\) nên \(AB' \bot BC\) Ta có \(AB' \bot SB\) và \(AB' \bot BC\) nên \(AB' \bot \left( {SBC} \right)\) Suy ra \(AB' \bot SC\). Theo giả thiết \(SC \bot AC'\), \(SC \bot AB'\) (chứng minh trên) \( \Rightarrow SC \bot \left( {AB'C'} \right)\) LG c Tính thể tích khối chóp \(S.AB’C’\). Lời giải chi tiết: Ta có \(AC’\) là đường cao trong tam giác vuông \(SAC\) nên \({{SC'} \over {SC}} = {{SC'.SC} \over {S{C^2}}} = {{S{A^2}} \over {S{C^2}}} = {{{a^2}} \over {3{a^2}}} = {1 \over 3}\) Từ đó suy ra \({{{V_{S.AB'C'}}} \over {{V_{S.ABC}}}} = {{SA} \over {SA}}.{{SB'} \over {SB}}.{{SC'} \over {SC}} = {1 \over 2}.{1 \over 3} = {1 \over 6}\) Vì \({V_{S.ABC}} = {{{a^3}} \over 6}\) nên \({V_{S.AB'C'}} = {{{a^3}} \over {36}}\). Cách khác: Vì SC'⊥AB'C' nên:
(trung tuyến trong tam giác vuông)
Thay (1), (2), (3) vào (*) ta được:
Nhận xét: Ta có: AB'⊥(SBC) nên có thể lấy V = (1/3)AB'.SΔSB'C'=(1/6). AB'.B' C'.SC' rồi tính toán. HocTot.XYZ
|