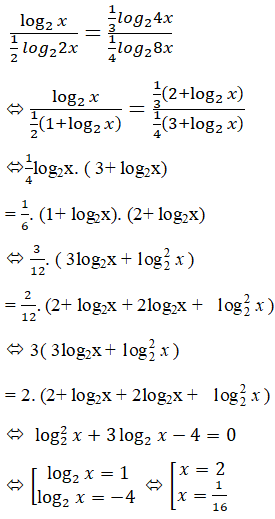Bài 69 trang 124 SGK giải tích 12 nâng caoGiải các phương trình sau:
Lựa chọn câu để xem lời giải nhanh hơn
Giải các phương trình sau: LG a \(\eqalign{ Lời giải chi tiết: Điều kiện: \(x> 0\) \(\eqalign{ Vậy \(S = \left\{ {10;\root 9 \of {10} } \right\}\) Chú ý: Có thể đặt \(t=\log x\) để giải phương trình như sau: \(\begin{array}{l} LG b \(\,{{{{\log }_2}x} \over {{{\log }_4}2x}} = {{{{\log }_8}4x} \over {{{\log }_{16}}8x}}\) Lời giải chi tiết: \({{{{\log }_2}x} \over {{{\log }_4}2x}} = {{{{\log }_8}4x} \over {{{\log }_{16}}8x}}\,\,\,\,\,\left( 1 \right)\) Điều kiện: \(x > 0\), \(x \ne {1 \over 2},\,x \ne {1 \over 8}\) \(\eqalign{ Đặt \(t = {\log _2}x\) thì (1) thành: \(\dfrac{t}{{\frac{{1 + t}}{2}}} = \dfrac{{\frac{{2 + t}}{3}}}{{\frac{{3 + t}}{4}}}\) \( \Leftrightarrow t.\frac{{3 + t}}{4} = \frac{{1 + t}}{2}.\frac{{2 + t}}{3}\) \( \Leftrightarrow 6t\left( {3 + t} \right) = 4\left( {1 + t} \right)\left( {2 + t} \right)\) \(\eqalign{ Vậy \(S = \left\{ {2;{1 \over {16}}} \right\}\) Chú ý: Có thể trình bày như sau:
LG c \(\eqalign{& \,{\log _{9x}}27 - {\log _{3x}}243 = 0 \cr} \) Lời giải chi tiết: Điều kiện: \(x > 0\); \(x \ne {1 \over 9},\,x \ne {1 \over 3}\) \(\Leftrightarrow {1 \over {{{\log }_{27}}9x}} - {1 \over {{{\log }_3}3x}} + {\log _{{3^2}}}{3^5} = 0\) \(\eqalign{ Đặt \({\log _3}x = t\) \(\eqalign{ Vậy \(S = \left\{ {{3^{ - 3}};{3^{ - 0,8}}} \right\}\) HocTot.XYZ
|