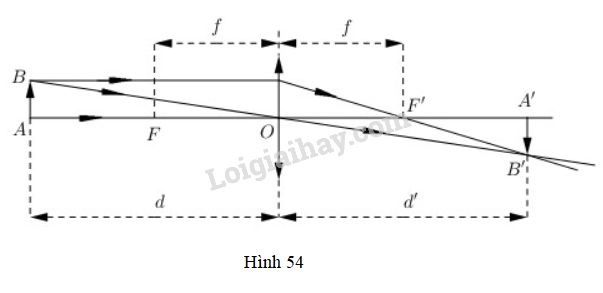
Bài 7 trang 133 SGK Đại số và Giải tích 11Một thấu kính hội tụ có tiêu cự là f. Video hướng dẫn giải Một thấu kính hội tụ có tiêu cự là \(f\). Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ một vật thật \(AB\) và từ ảnh \(A'B'\) của nó tới quang tâm \(O\) của thấu kính (h.54). Công thức thấu kính là \(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}.\)
LG a Tìm biểu thức xác định hàm số \(d' = φ(d)\). Phương pháp giải: Sử dụng công thức \(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f}\). Lời giải chi tiết: \(\dfrac{1}{d} + \dfrac{1}{{d'}}= \dfrac{1}{f}\) \( \Leftrightarrow \dfrac{1}{{d'}} = \dfrac{1}{f} - \dfrac{1}{d} \) \(\Leftrightarrow \dfrac{1}{{d'}} = \dfrac{{d - f}}{{fd}} \) \(\Leftrightarrow d' = \dfrac{{fd}}{{d - f}}\) Vậy \(d' = φ(d) = \dfrac{fd}{d-f}\). LG b Tìm \(\underset{d\rightarrow f^{+} }{\lim} φ(d)\), \(\underset{d\rightarrow f^{-} }{\lim} φ(d)\) và \(\underset{d\rightarrow +\infty }{\lim} φ(d)\). Giải thích ý nghĩa của các kết quả tìm được. Phương pháp giải: Sử dụng quy tắc tìm giới hạn của thương. Lời giải chi tiết: \(\begin{array}{l} Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực. \(\begin{array}{l} Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực. +) \(\underset{d\rightarrow +\infty }{\lim} φ(d) \) \(=\underset{d\rightarrow +\infty }{\lim}\) \(\dfrac{fd}{d-f}\) = \(\underset{d\rightarrow +\infty }{\lim}\) \(\dfrac{f}{1-\dfrac{f}{d}} = f\). Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính). HocTot.XYZ
|