Đề bài

Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = {x^3} - 3{x^2} + 1$ là:

A.

$y = - 2x + 1$
B.

$y = 2x - 1$
C.

$y = - 2x - 1$
D.

$y = 2x + 1$

Phương pháp giải

Cách 1:

+) Tìm các điểm cực trị của đồ thị hàm số theo quy tắc 1:

Quy tắc 1:

- Bước 1: Tìm tập xác định của hàm số.

- Bước 2: Tính $f'\left( x \right)$, tìm các điểm tại đó $f'\left( x \right) = 0$ hoặc không xác định.

- Bước 3: Lập bảng biến thiên và kết luận.

+ Tại các điểm mà đạo hàm đổi dấu từ âm sang dương thì đó là điểm cực tiểu của hàm số.

+ Tại các điểm mà đạo hàm đổi dấu từ dương sang âm thì đó là điểm cực đại của hàm số.

+) Thay tọa độ 2 cực trị vừa tìm vào phương trình y = ax + b và tìm hệ số a, b. Từ đó suy ra phương trình đường thẳng.

Cách 2:

Muốn tìm phương trình đường thẳng đi qua hai điểm cực trị của hàm số ta lấy $y$ chia cho $y’$ và lấy phần dư.

Cách 3: Sử dụng MTCT cho hàm bậc 3 (Chỉ sử dụng khi đã được học chương số phức).

Bước 1: Tính y' và y''.

Bước 2: Bấm máy và sử dụng chức năng CALC.

Mode 2 và nhập: $y-\dfrac{y'.y''}{18a}$.

Trong đó a là hệ số của $x^3$.

Bấm tiếp: CALC + SHIFT+ "$i$" "=".

Với $i$ là đơn vị ảo (số phức) trên máy tính.

Bước 3: Kết luận.

Kết quả nhận được có dạng $ a+bi $ thì phương trình đường thẳng cần tìm là $y=bx+a$.

Lời giải của GV HocTot.XYZ

Cách 1:

$y' = 3{x^2} - 6x$.

$y' = 0 \Leftrightarrow 3x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \Rightarrow y = 1 \hfill \\x = 2 \Rightarrow y = - 3 \hfill \\ \end{gathered} \right.$

Từ đây suy ra hai điểm cực trị có tọa độ $A\left( {0;1} \right)$ và $B\left( {2; - 3} \right)$.

Đường thẳng cần tìm có dạng $y = ax + b$. Thay tọa độ 2 điểm cực trị A, B của đồ thị vào phương trình, ta được:

$\left\{ \begin{array}{l}1 = a.0 + b\\ - 3 = a.2 + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 1\\a = - 2\end{array} \right.$

Vậy đường thẳng đi qua 2 điểm cực trị trên là $y = - 2x + 1$.

Cách 2:

Ta có $y' = 3{x^2} - 6x$.

Khi đó ${x^3} - 3{x^2} + 1 $ $= \left( {3{x^2} - 6x} \right)\left( {\dfrac{1}{3}x - \dfrac{1}{3}} \right) - 2x + 1$.

Vậy đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là $y = - 2x + 1$.

Cách 3:

Bước 1:

$y'=3x^2-6x$; $y''=6x-6$

Bước 2:

Mode 2 và nhập: $y-\dfrac{y'.y''}{18a}$.

Trong đó a là hệ số của $x^3$.

Bấm tiếp: CALC + SHIFT+ "$i$" "=".

Với $i$ là đơn vị ảo (số phức) trên máy tính.

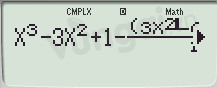
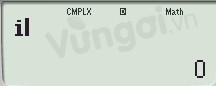
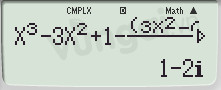
Bước 3: Ta được $a = 1$ và $b = -2$.

Vậy đường thẳng là: $y=-2x+1$.

Đáp án : A

Báo lỗi - Góp ý

Các bài tập cùng chuyên đề