Nội dung từ Loigiaihay.Com
Cho \(\Delta\)ABC có AB = AC và MB = MC (\(M \in BC\)).Chọn câu sai.
-
A.
\(\Delta AMC = \Delta BCM\)
-
B.
\(AM \bot BC\)
-
C.
\(\widehat {BAM} = \widehat {CAM}\)
-
D.
\(\Delta AMB = \Delta AMC\)
2 tam giác có 3 cặp cạnh tương ứng bằng nhau thì 2 tam giác đó bằng nhau. ( c.c.c)
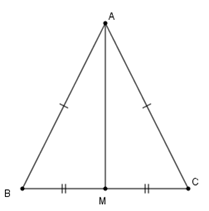
Xét \(\Delta AMB\) và \(\Delta AMC\) có
\(AB = AC\,\left( {gt} \right)\)
\(MB = MC\left( {gt} \right)\)
Cạnh \(AM\) chung
Nên \(\Delta AMB = \Delta AMC\,\left( {c - c - c} \right)\)
Suy ra \(\widehat {BAM} = \widehat {CAM}\) và \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng bằng nhau)
Mà \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {AMB} = \widehat {AMC} = \frac{{180^\circ }}{2} = 90^\circ .\) Hay \(AM \bot BC.\)
Vậy B, C, D đúng, A sai.
Đáp án : A

Các bài tập cùng chuyên đề
Bài 1 :
Vẽ tam giác ABC có \(AB = 5\;{\rm{cm}},AC = 4\;{\rm{cm}}\), \(BC = 6\;{\rm{cm}}\) theo các bước sau:
- Dùng thước thẳng có vạch chia vẽ đoạn thẳng \(BC = 6\;{\rm{cm}}\).
- Vẽ cung tròn tâm \(B\) bán kính \(5\;{\rm{cm}}\) và cung tròn tâm \(C\) bán kính \(4\;{\rm{cm}}\) sao cho hai cung tròn cắt nhau tại điểm \(A({\rm{H}}.4.14)\).
- Vẽ các đoạn thẳng A B, A C ta được tam giác ABC.
Bài 2 :
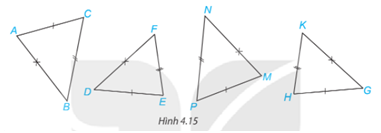
Trong Hình 4.15, những cặp tam giác nào bằng nhau?
Bài 3 :
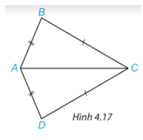
Cho hình 4.17, biết AB=AD, BC=DC. Chứng minh rằng \(\Delta ABC = \Delta ADC\)
Bài 4 :
Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy
1.Vẽ đường tròn tâm O, cắt Ox và Oy lần lượt tại A và B.
2.Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.
3. Vē tia Oz đi qua M.
Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.
Bài 5 :
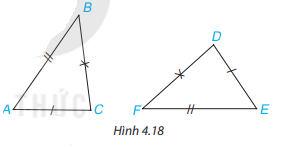
Cho tam giác ABC và DEF như hình 4.18. Trong các khẳng định sau, khẳng định nào đúng?
(1)\(\Delta ABC = \Delta DEF\)
(2) \(\Delta ACB = \Delta EDF\)
(3) \(\Delta BAC = \Delta DFE\)
(4)\(\Delta CAB = \Delta DEF\)
Bài 6 :
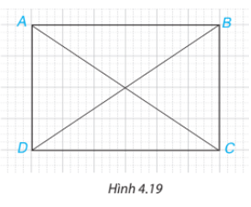
Trong Hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau.
Bài 7 :
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE\), \(AC = DF\), \(\widehat {BAC} = \widehat {EDF} = {60^\circ }\), \(BC = 6\;{\rm{cm}}\), \(\widehat {ABC} = {45^\circ }\). Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.
Bài 8 :
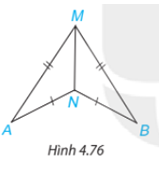
Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng\(\widehat {MAN} = \widehat {MBN}\).
Bài 9 :
Trong mỗi hình vẽ trên lưới ô vuông dưới đây, hãy chỉ ra một cặp hai tam giác bằng nhau.
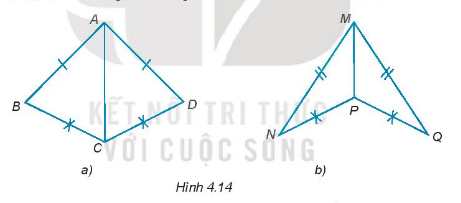
Bài 10 :
Cho hình 4.14, chứng minh rằng \(\Delta ABC = \Delta ADC;\Delta MNP = \Delta MQP.\)
Bài 11 :
Cho hình 4.15, chứng minh rằng \(\Delta ABC = \Delta DCB;\Delta ADB = \Delta DAC\)
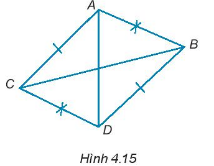
Bài 12 :
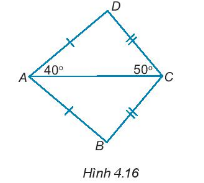
Cho hình 4.16, biết rằng \(\widehat {DAC} = {40^0};\widehat {DCA} = {50^0}\), hãy tính số đo các góc của tam giác ABC.
Bài 13 :
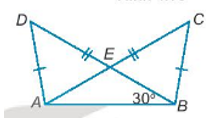
Cho hình 4.17, biết rằng AD = BC, AC = BD và \(\widehat {ABD} = {30^0}\), hãy tính số đo của góc DEC.
Bài 14 :
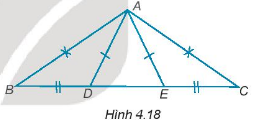
Cho các điểm A, B, C, D, E như hình 4.18, biết rằng AB = AC, AD = AE, BD = CE. Chứng minh rằng \(\widehat {AEB} = \widehat {ADC}\)
Bài 15 :
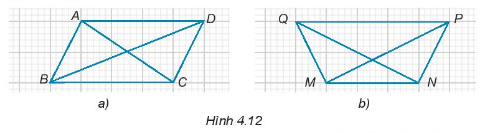
Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (H.4.19)
Chứng minh \(\Delta ABD = \Delta DCA;\Delta ADC = \Delta BCD.\)
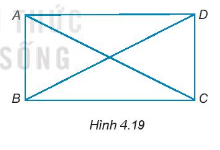
Bài 16 :
Cho các điểm A, B, C, D như Hình 4.57
a) Chứng minh rằng \(\widehat {DAC} = \widehat {DBC}\).
b) Đường thẳng DC có vuông góc với đường thẳng AB không? Vì sao?
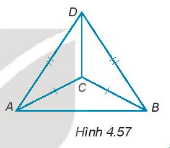
Bài 17 :
Cho các điểm A, B, C, D như hình vẽ bên.
a) Chứng minh \(\Delta ABD = \Delta CBD\)
b) Biết rằng \(\widehat {BAD} = {90^o},\widehat {CDB} = {30^o}\), hãy tính \(\widehat {ABC}\).
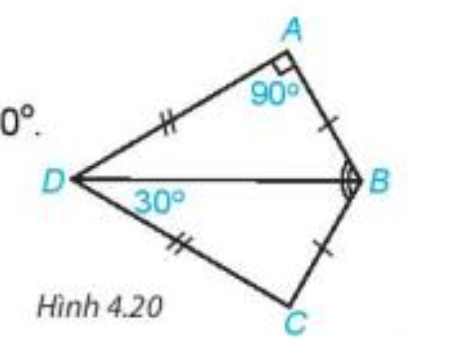
Bài 18 :
Cho các điểm A, B, C, D như hình vẽ. Biết rằng \(\widehat {DAC} = {60^o}\). Hãy tính \(\widehat {DAB}\).
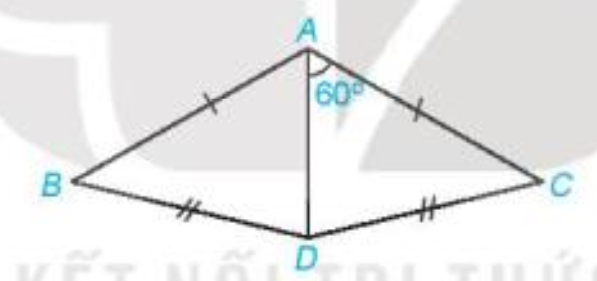
Bài 19 :
Cho các điểm A, B, C, D như hình dưới đây. Biết \(\Delta ADC = \Delta BCD\), hãy chứng minh \(\Delta ADB = \Delta BCA\).
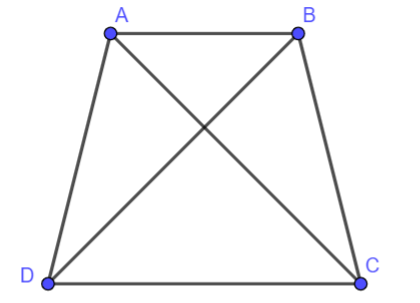
Bài 20 :
Trong hình vẽ sau, ta có AM = BM, AN = BN. Chứng minh rằng
\(\widehat {MAN} = \widehat {MBN}\)
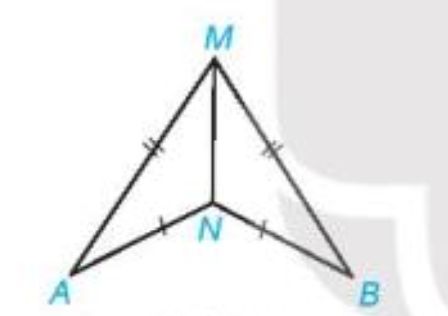
Bài 21 :
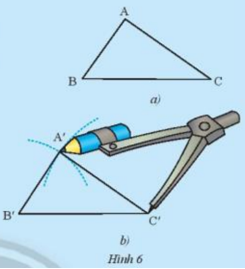
Cho tam giác ABC như trong Hình 6a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có ba cạnh bằng ba cạnh của tam giác ABC (A’B’= AB, A’C’= AC, B’C’= BC) theo các bước:
-Vẽ đoạn thẳng B’C’= BC
-Vẽ cung tròn tâm B’có bán kính bằng BA, vẽ cung trong tâm C’ có bán kính bằng CA.
-Hai cung tròn trên cắt nhau tại A’ (chỉ lấy một trong hai giao điểm của hai cung)
-Vẽ các đoạn thẳng B’A, C’A’, ta được tam giác A’B’C’ (Hình 6b)
Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’ lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Bài 22 :
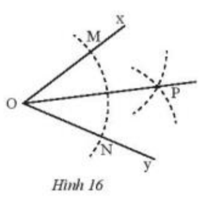
Cho \(\widehat {xOy}\). Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau tại điểm P nằm trong \(\widehat {xOy}\). Nối O với P (Hình 16). Hãy chứng minh rằng , từ đó suy ra OP là tia phân giác của \(\widehat {xOy}\).
Bài 23 :
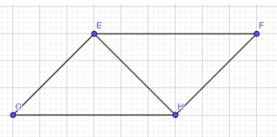
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
a) \(\Delta EFH=\Delta HGE\)
b) EF // HG
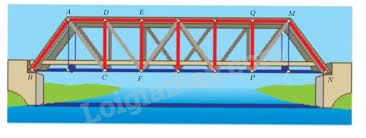
Bài 24 :
Đặt tên cho một số điểm có trong Hình 26 và chỉ ra ba cặp tam giác bằng nhau trong hình đó.
Bài 25 :
Giá để đồ ở Hình 33 gợi nên hình ảnh hai tam giác ABC và A’B’C’ có: AB = A’B’, BC = B’C’, CA = C’A’.
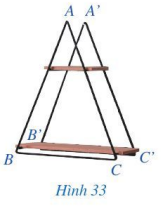
Tam giác ABC có bằng tam giác A’B’C’ hay không?
Bài 26 :
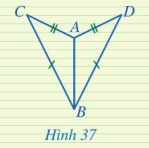
Hai tam giác ở Hình 37 có bằng không? Vì sao?
Bài 27 :
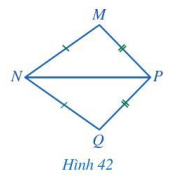
Cho Hình 42 có MN = QN, MP = QP. Chứng minh \(\widehat {MNP} = \widehat {QNP}\).
Bài 28 :
Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP, \(\widehat A = 65^\circ ,\widehat N = 71^\circ \). Tính số đo các góc còn lại của hai tam giác.
Bài 29 :
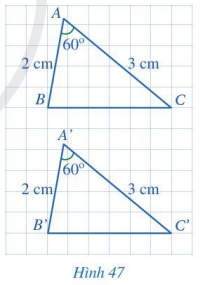
Cho hai tam giác ABC và A’B’C’ (Hình 47) có: AB = A’B’ = 2 cm, \(\widehat A = \widehat {A'} = 60^\circ \), AC = A’C’ = 3 cm. Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
Bài 30 :
Cho tam giác ABC và DEH trong hình dưới đây.
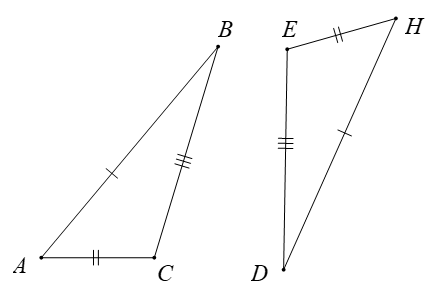
Khẳng định đúng là
-
A.
∆ABC = ∆DEH;
-
B.
∆ABC = ∆HDE;
-
C.
∆ABC = ∆EDH;
-
D.
∆ABC = ∆HED.