Nội dung từ Loigiaihay.Com
Cho \(\Delta ABC\) vuông tại $A,$ có \(\widehat C = {30^0}\), đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:
-
A.
$BM$ là đường trung tuyến của \(\Delta ABC\)
-
B.
\(BM = AB\).
-
C.
$BM$ là phân giác của \(\widehat {ABC}\).
-
D.
$BM$ là đường trung trực của \(\Delta ABC\).
Áp dụng tính chất tam giác cân, tính chất đường trung trực của đoạn thẳng, định lý tổng 3 góc trong tam giác
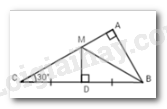
Vì $M$ thuộc đường trung trực của $BC$ nên \( BM = MC\) (tính chất đường trung trực của đoạn thẳng)
Suy ra \(\Delta BMC\) cân tại $M$ (dấu hiệu nhận biết tam giác cân)
Do đó \( \widehat {MBC} = \widehat C = {30^0}\) (tính chất tam giác cân)
Xét \(\Delta ABC\) có:
\(\widehat A + \widehat {ABC} + \widehat C = {180^0}\) (định lý tổng 3 góc trong tam giác)
Suy ra \(\widehat {ABC} = {180^0} - \widehat C - \widehat A = {180^0} - {30^0} - {90^0} = {60^0}\)
Dẫn đến \(\widehat {ABM} + \widehat {MBC} = \widehat {ABC} = {60^0} \)
Nên \(\widehat {ABM} = {60^0} - \widehat {MBC} = {60^0} - {30^0} = {30^0}\)
Suy ra \( \widehat {ABM} = \widehat {MBC}\) hay $BM$ là phân giác của \(\widehat {ABC}\).
Đáp án : C

Các bài tập cùng chuyên đề
Bài 1 :
Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.
Bài 2 :
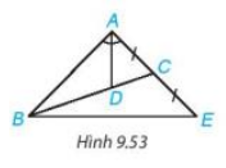
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD= 2 DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A
Gợi ý D là trọng tâm của tam giác ABE, tam giác này có đường phân giác AD đồng thời là trung tuyến.
Bài 3 :
Cho tam giác ABC cân tại A (\(\widehat A < {90^o}\)). Hai đường cao BE và CF cắt nhau tại H.
a) Chứng minh rẳng \(\Delta BFC = \Delta CEB\)
b) Chứng minh rằng \(\Delta AEH = \Delta AFH\)
c) Gọi I là trung điểm BC. Chứng minh rằng ba điểm A,H,I thẳng hàng.
Bài 4 :
Cho tam giác nhọn ABC (AB < AC), vẽ đường cao AH. Đường trung trực của BC cắt AC tại M, cắt BC tại N.
a) Chứng minh rằng \(\widehat {BMN} = \widehat {HAC}\)
b) Kẻ \(MI \bot AH\)(I ∈ AH), gọi K là giao điểm của AH và BM. Chứng minh rằng I là trung điểm của AK.
Bài 5 :
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng;
b) Nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.
Bài 6 :
Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh \(\widehat {BAC} = {45^0}\).
Bài 7 :
a) Giả sử đường trung trực d của cạnh BC của tam giác ABC cắt cạnh AC tại một điểm D nằm giữa A và C. Chứng minh AC > AB.
b) Hỏi đảo lại có đúng không tức là nếu tam giác ABC có AC > AB thì đường trung trực d của cạnh BC có cắt AC tại điểm nằm giữa A và C không?
c) Vẫn giả sử đường trung trực d của cạnh BC của tam giác ABC cắt cạnh AC tại một điển D nằm giữa A và C. Với M là một điểm tuỳ ý thuộc d, M khác D, hãy chứng minh MA + MB > DA + DB.
Bài 8 :
Cho M là một điểm tuỳ ý bên trong tam giác đều ABC. Lấy điểm N nằm khác phía với M đối với đường thẳng AC sao cho \(\widehat {CAN} = \widehat {BAM}\) và AN = AM.
Chứng minh:
a) Tam giác AMN là tam giác đều
b) \(\Delta MAB = \Delta NAC\)
c) MN = MA, NC = MB
Bài 9 :
Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác của góc A. Chứng minh tam giác ABC là tam giác cân.
Bài 10 :
Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác và gọi I là giao điểm của các đường phân giác của tam giác. Chứng minh ba điểm A, I, G thẳng hàng.
Bài 11 :
Cho tam giác nhọn ABC. Hãy nêu cách tìm các điểm sau đây bên trong tam giác ABC.
a) Điểm M cách đều ba đỉnh của tam giác ABC.
b) Điểm N cách đều ba cạnh của tam giác ABC
c) Điểm P là trọng tâm của tam giác ABC.
d) Điểm Q là trực tâm của tam giác ABC.
Bài 12 :
Cho tam giác đều ABC có I là điểm cách đều ba cạnh AB, BC, CA. Chứng minh rằng I cách đều ba đỉnh A, B, C và cũng là trọng tâm của tam giác ABC.
Bài 13 :
Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AB = AD. Vẽ BE vuông góc với CD tại E. Gọi I là giao điểm của AC và BE; K là hình chiếu của I trên BC.
a) Chứng minh ba điểm D, I, K thẳng hàng.
b) Tìm điều kiện của tam giác ABC để I là trọng tâm của tam giác BCD.
Bài 14 :
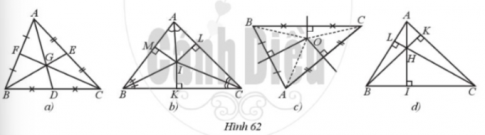
Trong các hình 62a, 62b, 62c, 62d, hình nào có điểm cách đều các đỉnh của tam giác đó? Vì sao?
Bài 15 :
Cho tam giác ABC cân tại A có các đường cao BD và CE cắt nhau tại H.
a) Chứng minh ∆ADB = ∆AEC.
b) Chứng minh tam giác HDE là tam giác cân.
c) So sánh HB và HD.
d) Gọi M là trung điểm của HC, N là trung điểm của HB, I là giao điểm của BM và CN. Chứng minh ba điểm A, H, I thẳng hàng.
Bài 16 :
Cho \(\Delta ABC\) vuông tại A. Tia phân giác của \(\widehat {ABC}\) cắt AC tại E. Từ E kẻ \(EH \bot BC\) tại H và EH cắt AB tại K.
a) Chứng minh \(AE = EH\).
b) So sánh độ dài hai cạnh AE và EC.
c) Chứng minh BE là đường trung trực của AH.
d) Chứng minh \(\Delta KBC\) là tam giác cân.
Bài 17 :
Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.
Bài 18 :
Cho tam giác ABC cân tại A, đường cao AH \(\left( {H \in BC} \right)\).
a) Chứng minh \(\Delta AHB = \Delta AHC\).
b) Từ H kẻ đường thẳng song song với AC, cắt AB tại D. Chứng minh \(AD = DH\).
c) Gọi M là trung điểm của AC, CD cắt AH tại G. Chứng minh ba điểm B, G, M thẳng hàng.
d) Chứng minh chu vi \(\Delta ABC\) lớn hơn \(AH + 3BG\).
Bài 19 :
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho \(BD = 2DC\). Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.47). Chứng minh rằng tam giác ABE cân tại A.
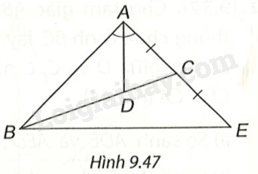
Gợi ý. D là trọng tâm của tam giác ABE, tam giác này có đường phân giác AD đồng thời là đường trung tuyến.
Bài 20 :
Cho tam giác ABC cân tại A. Trên tia đối của tia BC và tia đối của tia CB theo thứ tự lấy hai điểm D và E sao cho \(BD = CE\).
a) Chứng minh \(\Delta ADE\) cân.
b) Gọi M là trung điểm của BC. Chứng minh AM là tia phân giác của góc DAE và \(AM \bot DE\).
c) Từ B và C kẻ BH, CK theo thứ tự vuông góc với AD, AE. Chứng minh: \(BH = CK\).
d) Chứng minh: HK//BC.
Bài 21 :
Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho \(BD = BA\) và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt BA tại M. Chứng minh rằng:
a) \(\Delta ABH = \Delta DBH\).
b) Tam giác AED cân.
c) \(EM > ED\).
d) Tam giác BCM là tam giác đều và \(CE = 2EA\), biết \(\widehat {ABC} = {60^o}\).
Bài 22 :
Nếu tam giác \(ABC\) cân tại B thìA. Đường trung tuyến AM đồng thời là đường phân giác
B. Đường trung tuyến CP đồng thời là đường trung trực
C. Đường trung tuyến BN đồng thời là đường phân giác
D. Đường trung tuyến AM đồng thời là đường trung trực
Bài 23 :
Cho tam giác \(ABC\) cân tại \(A\), kẻ \(AH\)vuông góc với \(BC\)\(\left( {H \in BC} \right)\). Gọi \(P\) là trung điểm của \(HC\). Trên tia đối của tia \(PA\) lấy điểm \(Q\) sao cho \(QP = PA\).a) Chứng minh rằng: \(\Delta APH = \Delta QPC\) và \(QC\) vuông góc với\(BC\).
b) Chứng minh rằng: \(QC = AH\) từ đó suy ra \(AC > QC\).
c) Chứng minh rằng: \(\angle PAC < \angle HAP\)
d) Gọi \(I\) là trung điểm của \(BQ\). Chứng minh rằng ba điểm \(A,H,I\) thẳng hàng.
Bài 24 :
Cho \(\Delta ABC\) cân tại \(A\), tia phân giác của \(\angle BAC\) cắt cạnh \(BC\)tại \(D\). Kẻ \(DH\) vuông góc với \(AB\) tại \(H\), kẻ \(DK\) vuông góc với \(AC\) tại \(K\).a) Chứng minh: \(\Delta AHD = \Delta AKD\)
b) Tia \(KD\) cắt tia \(AB\) tại \(M\), tia \(HD\) cắt tia \(AC\) tại \(N\). Chứng minh: \(HM = KN\)
c) Chứng minh: \(AD \bot MN\) và \(BC//MN\)
d) Gọi \(I\) là giao điểm của \(AD\) và \(MN\). Qua \(I\) kẻ đường thẳng d song song với \(AM\), đường thẳng \(d\) cắt \(AN\)tại \(E\). Chứng minh: \(IE = \dfrac{1}{2}AM\)
Bài 25 :
Cho tam giác $ABC$ cân tại $A$, kẻ $AH$ vuông góc với $BC$$\left( {H \in BC} \right)$. Gọi $P$ là trung điểm của $HC$. Trên tia đối của tia $PA$ lấy điểm $Q$ sao cho $QP = PA$.a) Chứng minh rằng: $\Delta APH = \Delta QPC$ và $QC$ vuông góc với$BC$.
b) Chứng minh rằng: $QC = AH$từ đó suy ra $AC > QC$.
c) Chứng minh rằng: $\angle PAC < \angle HAP$
d) Gọi $I$ là trung điểm của $BQ$. Chứng minh rằng ba điểm $A,H,I$ thẳng hàng.
Bài 26 :
Cho tam giác \(ABC\) cân tại \(A\), kẻ \(AH\)vuông góc với \(BC\)\(\left( {H \in BC} \right)\). Gọi \(P\) là trung điểm của \(HC\). Trên tia đối của tia \(PA\) lấy điểm \(Q\) sao cho \(QP = PA\).a) Chứng minh rằng: \(\Delta APH = \Delta QPC\) và \(QC\) vuông góc với\(BC\).
b) Chứng minh rằng: \(QC = AH\) từ đó suy ra \(AC > QC\).
c) Chứng minh rằng: \(\angle PAC < \angle HAP\)
d) Gọi \(I\) là trung điểm của \(BQ\). Chứng minh rằng ba điểm \(A,H,I\) thẳng hàng.
Bài 27 :
Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AD = AB.
a) Chứng minh rằng CBD là tam giác cân.
b) Gọi M là trung điểm của CD, đường thẳng qua D và song song với BC cắt đường thẳng BM tại E. Chứng minh rằng BC = DE và BC + BD > BE
c) Gọi G là giao điểm của AE và DM. Chứng minh rằng BC = 6GM
Bài 28 :
Cho tam giác ABC cân tại A có \(\widehat {ABC} = 70^\circ \). Vẽ AD vuông góc với BC (\(D \in BC\)).a) Tính số đo các góc còn lại của tam giác ABC.
b) Chứng minh: \(\Delta ADB = \Delta ADC\).
c) Gọi M là trung điểm của DB. Từ M vẽ đường thẳng vuông góc với BC cắt AB tại E. Chứng minh: DE // AC.
Bài 29 :
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H. Lấy N là trung điểm của cạnh AC, hai đoạn thẳng BN và AH cắt nhau tại G. Trên tia đối của tia NG lấy điểm K sao cho NK = NG.a) Chứng minh \(\Delta ABH = \Delta ACH\).
b) Chứng minh \(CK \bot BC\).
c) Gọi I là giao điểm của KH và CG. Chứng minh I là trọng tâm của \(\Delta BCK\).
d) Gọi M là trung điểm của cạnh AB. Chứng minh \(GM < \frac{1}{4}\left( {BC + AG} \right)\).
Bài 30 :
Cho tam giác ABC vuông tại A (AB < AC). Kẻ BD là tia phân giác của \(\widehat {ABC}\) (D \( \in \) AC).Trên cạnh BC lấy điểm E sao cho AB = BE.a) Chứng minh \(\Delta ABD = \Delta EBD\). Từ đó suy ra DA = DE.
b) So sánh DA và DC?
c) Đường thẳng ED cắt AB tại F. Gọi S là trung điểm của FC. Chứng minh ba: điểm B, D, S thẳng hàng.












