Nội dung từ Loigiaihay.Com
Miền nghiệm của bất phương trình \(3x + 2(y - 1) > 4(x + 1) - 3y\) chứa điểm có tọa độ:
-
A.
\((3;0)\)
-
B.
\((0;0)\)
-
C.
\((3;2)\)
-
D.
\((1; - 1)\)
Rút gọn bất phương trình.
Thay tọa độ từng điểm vào bất phương trình trên. Cặp (x;y) nào thỏa mãn bất phương trình thì thuộc miền nghiệm.
\(3x + 2(y - 1) > 4(x + 1) - 3y\)
\(3x + 2y - 2 > 4x + 4 - 3y\)
\(3x + 2y - 2 - 4x - 4 + 3y > 0\)
\( - x + 5y - 6 > 0\)
\( - x + 5y > 6\)
Ta thay tọa độ từng điểm vào bất phương trình trên. Cặp (x;y) nào thỏa mãn bất phương trình thì thuộc miền nghiệm.
Vì \( - 3 + 5.2 = 7 > 6\) nên điểm có tọa độ \((3;2)\) thuộc miền nghiệm.
Đáp án : C

Các bài tập cùng chuyên đề
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
Cặp số nào sau đây là nghiệm của bất phương trình \(3x - 5y > 12\)?
Miền nghiệm của bất phương trình \(x + 2(y + 1) - 4y \le 2(x + 1) - 5y\) không chứa điểm có tọa độ:
Điểm \(A(1;2)\) thuộc miền nghiệm của bất phương trình nào sau đây?
Miền nghiệm của bất phương trình \(x - y \le 2\) là phần không gạch trong hình nào dưới đây?
Phần không gạch chéo trong hình dưới đây biểu diễn miền nghiệm của bất phương trình nào?
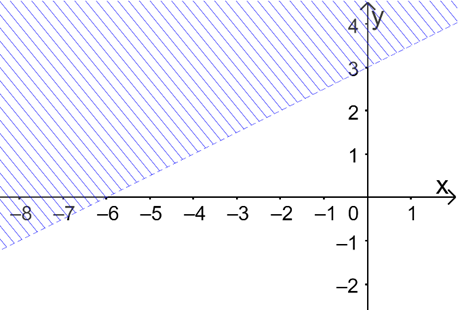
Cho bất phương trình \(2x + 3y - 6 \le 0\,\,(1)\). Chọn khẳng định đúng trong các khẳng định sau:
Cho \(x,y\) thoả mãn hệ \(\left\{ \begin{array}{l}x + 2y - 100 \le 0\\2x\,\, + \,y - 80\,\, \le 0\\x \ge 0\\y \ge 0\end{array} \right..\) Tìm giá trị lớn nhất \({P_{\max }}\) của biểu thức \(P = \left( {x;y} \right) = 40000x + 30000y.\)
Giá trị nhỏ nhất \({F_{\min }}\) của biểu thức \(F\left( {x;y} \right) = 4x + 3y\) trên miền xác định bởi hệ \(\,\left\{ \begin{array}{l}0 \le \,\,x\,\, \le \,\,10\\0\,\, \le \,\,y\,\, \le \,\,9\\2x\,\, + \,\,y\,\, \ge \,\,14\\2x\,\, + \,\,5y\,\, \ge \,\,30\end{array} \right.\) là
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo.
- Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu;
- Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu.
Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?












