Nội dung từ Loigiaihay.Com
Đề bài
Cho một góc lượng giác (Ox, Ou) có số đo \( - {30^o}\) và một góc lượng giác (Ox, Ov) có số đo \({120^o}\). Tính số đo góc lượng giác (Ou, Ov).
-
A.
\({150^o} + k{360^o}\) \((k \in \mathbb{Z})\)
-
B.
\({-150^o} + k{360^o}\) \((k \in \mathbb{Z})\)
-
C.
\({90^o} + k{360^o}\) \((k \in \mathbb{Z})\)
-
D.
\({-90^o} + k{360^o}\) \((k \in \mathbb{Z})\)
Phương pháp giải
Sử dụng hệ thức Chasles: Với ba tia Ou, Ov, Ow bất kì, ta có:
sđ (Ou,Ov) + sđ (Ov,Ow) = sđ (Ou,Ow) + \(k{360^o}\) \((k \in \mathbb{Z})\).
Lời giải của GV HocTot.XYZ
Ta có: sđ (Ox,Ov) = sđ (Ox,Ou) + sđ (Ou,Ov) + k360o.
Suy ra: sđ (Ou,Ov) = sđ (Ox,Ov) - sđ (Ox,Ou) + k360o
\( = {120^o} - ( - {30^o}) + k{360^o} = {150^o} + k{360^o}\).
Đáp án : A
Các bài tập cùng chuyên đề
Bài 1 :
Cho một góc lượng giác (Ox, Ou) có số đo \( - {30^o}\) và một góc lượng giác (Ox, Ov) có số đo \({120^o}\). Tính số đo góc lượng giác (Ou, Ov).
-
A.
\({150^o} + k{360^o}(k \in Z)\)
-
B.
\( - {150^o} + k{360^o}\) \((k \in Z)\)
-
C.
\({90^o} + k{360^o}\) \((k \in Z)\)
-
D.
\( - {90^o} + k{360^o}\) \((k \in Z)\)
Xem lời giải >>
Bài 2 :
Cho một góc lượng giác $(O x, O u)$ có số đo $240^{\circ}$ và một góc lượng giác $(O x, O v)$ có số đo $-270^{\circ}$. Tính số đo của các góc lượng giác $(O u, O v)$.
Xem lời giải >>
Bài 3 :
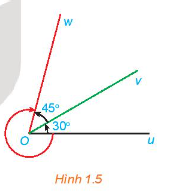
Cho ba tia Ou, Ov, Owvới số đo của các góc hình học uOv và vOw lần lượt là \({30^ \circ }\) và \({45^ \circ }\)
a) Xác định số đo của ba góc lượng giác \((Ou,Ov)\) ,\((Ov,Ow\) và \((Ou,Ow)\) được chỉ ra ở Hình 1.5.
b) Với các góc lượng giác ở câu a, chứng tỏ rằng có một số nguyên k để
sđ\((Ou,Ov)\) + sđ\((Ov,Ow\) = sđ \((Ou,Ow)\) + k\({.360^ \circ }\)
Xem lời giải >>
Bài 4 :
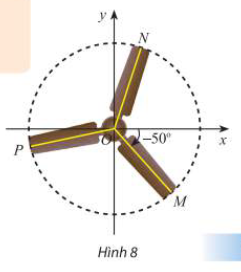
Trong Hình 8, chiếc quạt có ba cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox,ON) và (Ox,OP).
Xem lời giải >>
Bài 5 :
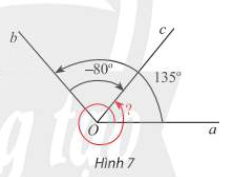
Cho Hình 7.
a) Xác định số đo các góc lượng giác (Oa,Ob), (Ob,Oc) và (Oa,Oc).
b) Nhận xét về mối liên hệ giữa ba số đo góc này.
Xem lời giải >>
Bài 6 :
Cho góc lượng giác \(\left( {Ou,Ov} \right)\) có số đo là \(\frac{\pi }{4}\). Số đo của các góc lượng giác nào sau đây có cùng tia đầu là \(Ou\) và tia cuối là \(Ov\)?
-
A.
\(\frac{{3\pi }}{4}\)
-
B.
\(\frac{{5\pi }}{4}\)
-
C.
\(\frac{{7\pi }}{4}\)
-
D.
\(\frac{{9\pi }}{4}\)
Xem lời giải >>