Cho hình chóp tam giác đều S.ABC có độ dài tất cả các cạnh bằng 4cm.  Gọi I. H lần lượt là trung điểm cạnh AB, SC. Tính độ dài IH

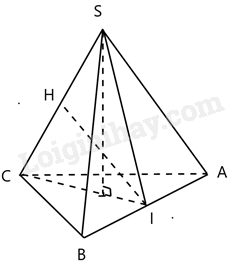
\(AI = IB = \frac{{AB}}{2} = 2cm\)

\(SH = HC = \frac{{SC}}{2} = \frac{4}{2} = 2cm\)

Tam giác ABC dều cạnh a nên CI là trung tuyến đồng thời là đường cao của tam giác ABC .

Áp dụng định lý Pythagore cho tam giác vuông CIA có

\(\begin{array}{l}C{I^2} + I{A^2} = A{C^2}\\ =  > C{I^2} = A{C^2} - I{A^2}\\ =  > C{I^2} = {4^2} - {2^2}\\ =  > CI = 2\sqrt 3 cm\end{array}\)

Tương tự áp dụng định lí Pythagore cho tam giác vuông SIB ta được: \(SI = 2\sqrt 3 cm\)

Xét tam giác SIC có: \(SI = IC = 2\sqrt 3 cm\)

\( \Rightarrow \)Tam giác SIC cân tại I

\( \Rightarrow \) IH vừa là trung tuyến đồng thời là đường cao của tam giác SIC cân.

Áp dụng định lý Pythagore cho tam giác vuông SIH có

\(\begin{array}{l}C{I^2} = I{H^2} + C{H^2}\\ =  > I{H^2} = C{I^2} - C{H^2}\\ =  > I{H^2} = {(2\sqrt 3 )^2} - {2^2}\\ =  > IH = 2\sqrt 2 cm\end{array}\)