Đề bài

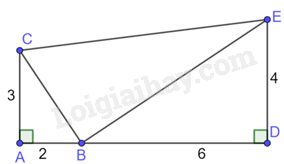
Cho hình vẽ:
Chọn đáp án đúng

A.
$CE = \sqrt {66}$
B.
$CE = \sqrt {65}$
C.
$CE = 8$
D.
$CE = 8,5$

Phương pháp giải

Sử dụng kiến thức trường hợp đồng dạng thứ hai của tam giác vuông: Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng.

Lời giải của GV HocTot.XYZ

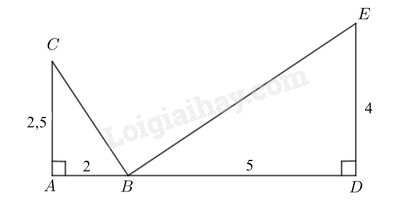
Ta có: $\frac{{AB}}{{DE}} = \frac{2}{4} = \frac{1}{2};\frac{{AC}}{{BD}} = \frac{3}{6} = \frac{1}{2}$ nên $\frac{{AB}}{{DE}} = \frac{{AC}}{{BD}}$

Tam giác ABC và tam giác DEB có: $\widehat {BAC} = \widehat {BDE} = {90^0},\frac{{AB}}{{DE}} = \frac{{AC}}{{BD}}$ nên $\Delta ABC \backsim \Delta DEB$

Do đó, $\widehat {CBA} = \widehat {BED}$

Mà $\widehat {BED} + \widehat {EBD} = {90^0}$ nên $\widehat {ABC} + \widehat {EBD} = {90^0}$

Mà $\widehat {ABC} + \widehat {EBD} + \widehat {CBE} = {180^0}$ nên $\widehat {CBE} = {90^0}$

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A có: $B{C^2} = A{B^2} + A{C^2} = 13$

Áp dụng định lý Pythagore vào tam giác BDE vuông tại D có: $B{E^2} = D{E^2} + B{D^2} = 52$

Áp dụng định lý Pythagore vào tam giác BCE vuông tại B có: $C{E^2} = B{E^2} + B{C^2} = 65$ nên $CE = \sqrt {65}$

Đáp án : B

Báo lỗi - Góp ý

Các bài tập cùng chuyên đề

Bài 1 :

Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: $\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}}$

Chọn đáp án đúng

A.
$\Delta ABC = \Delta DEF$
B.
$\Delta ABC \backsim \Delta DFE$
C.
$\Delta ABC \backsim \Delta EDF$
D.
$\Delta ABC \backsim \Delta DEF$

Xem lời giải >>

Bài 2 :

Hai tam giác vuông đồng dạng với nhau khi:

A.
Hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác kia
B.
Hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác kia
C.
Cả A, B đều đúng
D.
Cả A, B đều sai

Xem lời giải >>

Bài 3 :

Cho hình vẽ sau:

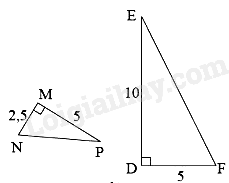
Chọn đáp án đúng.

A.
$\Delta MNP \backsim \Delta DFE$
B.
$\Delta MNP \backsim \Delta DEF$
C.
$\Delta MNP = \Delta DFE$
D.
Cả A, B, C đều sai

Xem lời giải >>

Bài 4 :

Cho tam giác ABC vuông tại A có: $AB = 3cm,AC = 5cm$ và tam giác MNP vuông tại M có $MN = 12cm,MP = 20cm.$ Khi đó,

A.
$\Delta ABC = \Delta MNP$
B.
$\Delta ABC \backsim \Delta MNP$
C.
$\Delta BAC \backsim \Delta MNP$
D.
$\Delta BCA \backsim \Delta MNP$

Xem lời giải >>

Bài 5 :

Cho hình vẽ:

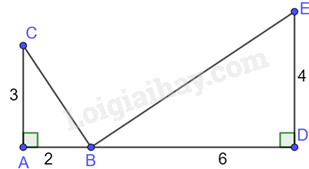
A.
$\Delta ABC \backsim \Delta DBE$
B.
$\Delta ABC \backsim \Delta DEB$
C.
$\Delta ABC \backsim \Delta EBD$
D.
Không có hai tam giác nào đồng dạng với nhau

Xem lời giải >>

Bài 6 :

Cho hình vẽ:

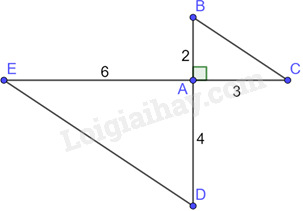
A.
$\widehat B = \widehat D$
B.
$\widehat B = \frac{2}{3}\widehat D$
C.
$\frac{2}{3}\widehat B = \widehat D$
D.
$\widehat B = \frac{3}{4}\widehat D$

Xem lời giải >>

Bài 7 :

Cho hình vẽ:

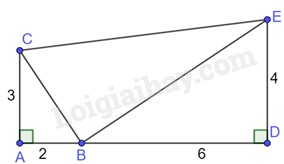
Chọn đáp án đúng

A.
$\widehat {ABC} + \widehat {EBD} = {80^0}$
B.
$\widehat {ABC} + \widehat {EBD} = {85^0}$
C.
$\widehat {ABC} + \widehat {EBD} = {95^0}$
D.
$\widehat {ABC} + \widehat {EBD} = {90^0}$

Xem lời giải >>

Bài 8 :

Cho hình vẽ dưới đây:

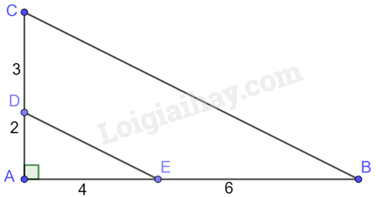
Chọn đáp án đúng

A.
$\widehat C = \frac{4}{3}\widehat {ADE}$
B.
$\frac{4}{3}\widehat C = \widehat {ADE}$
C.
$\widehat C = \widehat {ADE}$
D.
Cả A, B, C đều sai

Xem lời giải >>

Bài 9 :

Cho hình vẽ:

Khẳng định nào sau đây là đúng?

A.
$\widehat D + \widehat {ABC} = {85^0}$
B.
$\widehat D + \widehat {ABC} = {80^0}$
C.
$\widehat D + \widehat {ABC} = {90^0}$
D.
$\widehat D + \widehat {ABC} = {95^0}$

Xem lời giải >>

Bài 10 :

Cho hình vẽ:

Chọn đáp án đúng.

A.
$\widehat {BAH} = \widehat C$
B.
$\widehat {BAH} = \frac{2}{3}\widehat C$
C.
$\frac{2}{3}\widehat {BAH} = \widehat C$
D.
Cả A, B, C đều sai

Xem lời giải >>

Bài 11 :

Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có $\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}.$ Gọi M, M’ lần lượt là trung điểm của BC và B’C’. Khi đó, tỉ số $\frac{{AM}}{{A'M'}}$ bằng

A.
$\frac{1}{3}$
B.
$\frac{1}{4}$
C.
$\frac{1}{2}$
D.
$2$

Xem lời giải >>

Bài 12 :

Trên đoạn $BC = 13cm,$ đặt đoạn $BH = 4cm.$ Trên đường vuông góc với BC tại H, lấy điểm A sao cho $HA = 6cm$

Cho các khẳng định sau:

1. Số đo góc BAC bằng 80 độ

2. $AB.AC = AH.BC$

3. $\widehat B > \widehat {CAH}$

Có bao nhiêu khẳng định đúng?

A.
0
B.
1
C.
3
D.
2

Xem lời giải >>

Bài 13 :

Cho hình thang ABCD vuông tại A và D. Biết $CD = 2AB = 2AD = 2a$ và $BC = a\sqrt 2 .$ Gọi I là trung điểm của BC, H là chân đường vuông góc kẻ từ D xuống AC. Khi đó:

A.
$\widehat {HDI} = {45^0}$
B.
$\widehat {HDI} = {40^0}$
C.
$\widehat {HDI} = {50^0}$
D.
$\widehat {HDI} = {55^0}$

Xem lời giải >>

Bài 14 :

Cho O là trung điểm của đoạn AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ tia Ax, By cùng vuông góc với AB. Trên tia Ax lấy điểm C (khác A), qua O kẻ đường thẳng vuông góc với OC cắt tia By tại D. Kẻ OM vuông góc với CD tại M. Khi đó:

A.
$AC = \frac{4}{3}MC$
B.
$AC = \frac{3}{2}MC$
C.
$AC = \frac{2}{3}MC$
D.
$AC = MC$

Xem lời giải >>

Bài 15 :

Cho tam giác ABC vuông tại A có M là trung điểm của BC. Gọi I là hình chiếu của M trên AC. Chọn đáp án đúng.

A.
$\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{2}$
B.
$\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{3}$
C.
$\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{4}$
D.
$\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{2}{3}$

Xem lời giải >>

Bài 16 :

Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’ có chu vi bằng 30cm, các đường cao BH và B’H’. Biết rằng $\frac{{BH}}{{B'H'}} = \frac{{HC}}{{H'C'}} = \frac{3}{2}$ . Chu vi tam giác ABC là:

A.
15cm
B.
20cm
C.
30cm
D.
45cm

Xem lời giải >>

Bài 17 :

Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng $\frac{{BH}}{{B'H'}} = \frac{{HC}}{{H'C'}}$ . Biết rằng $\widehat {A'B'C'} = \frac{1}{7}\widehat {BAC}.$ Chọn đáp án đúng

A.
$\widehat {BAC} = {140^0}$
B.
$\widehat {BAC} = {100^0}$
C.
$\widehat {BAC} = {120^0}$
D.
$\widehat {BAC} = {110^0}$

Xem lời giải >>

Bài 18 :

Cho hình thang vuông ABCD, $\left( {\widehat A = \widehat D = {{90}^0}} \right)$ có $AB = 4cm,CD = 9cm$ và $BC = 13cm.$ Khoảng cách từ M đến BC bằng:

A.
4cm
B.
5cm
C.
6cm
D.
7cm

Xem lời giải >>

Bài 19 :

Cho tam giác ABC vuông tại A, $AC = 3AB = 3a.$ Lấy các điểm D, E thuộc AC sao cho $AD = DE = EC.$ Khi đó,

A.
$\widehat {AEB} + \widehat {ACB} = {40^0}$
B.
$\widehat {AEB} + \widehat {ACB} = {45^0}$
C.
$\widehat {AEB} + \widehat {ACB} = {50^0}$
D.
$\widehat {AEB} + \widehat {ACB} = {55^0}$

Xem lời giải >>

Bài 20 :

Cho hình thang vuông ABCD $\left( {\hat A = \hat D = {{90}^0}} \right)$ có AB = 4cm, CD = 9cm, BC = 13cm. Gọi M là trung điểm của AD. Tính $\widehat {BMC}$ .

A.
${60^0}$
B.
${110^0}$
C.
${80^0}$
D.
${90^0}$

Xem lời giải >>

Bài 21 :

Các tam giác vuông AHB và A'H'B' mô tả hai con dốc có chiều dài lần lượt là AB=13m, A′B′=6,5m và độ cao lần lượt là BH=5m, B′H′=2,5m. Độ dốc của hai con dốc lần lượt được tính bởi số đo các góc HAB và H'A'B'

- Nhận xét về hai đại lượng $\frac{{A'H'}}{{AB}} = \frac{{B'H'}}{{BH}}$

- Dùng định lí Pythagore để tính AH và A'H'

- So sánh các đại lượng $\frac{{A'H'}}{{AH}} = \frac{{B'H'}}{{BH}}$

- Hai tam giác vuông A'H'B' và AHB có đồng dạng không

Xem lời giải >>

Bài 22 :

Cho hai tam giác ABC và A’B’C’ có $\widehat {A'} = \widehat A = 90^\circ ,\,\,\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}$ (Hình 72). Chứng minh $\Delta A'B'C' \backsim \Delta ABC$

Xem lời giải >>

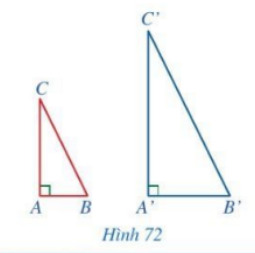
Bài 23 :

Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ sao cho $\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}$ . Chứng minh $\widehat B = \widehat {B'}$ .

Xem lời giải >>

Bài 24 :

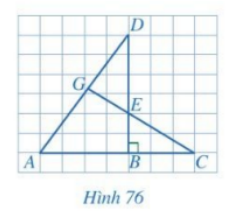
Cho Hình 76, biết $AB = 4,\,\,BC = 3,\,\,BE = 2,\,\,BD = 6$ . Chứng minh:

a) $\Delta ABD \backsim \Delta EBC$

b) $\widehat {DAB} = \widehat {DEG}$

c) Tam giác DGE vuông

Xem lời giải >>

Bài 25 :

Cho Hình 77, chứng minh

a) $\widehat {ABC} = \widehat {BED}$

b) $BC \bot BE$

Hình 77

Xem lời giải >>

Bài 26 :

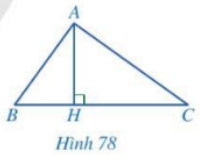
Cho Hình78, biết $A{H^2} = BH.CH$ . Chứng minh:

a) $\Delta HAB \backsim \Delta HCA$

b) Tam giác ABC vuông tại A.

Xem lời giải >>

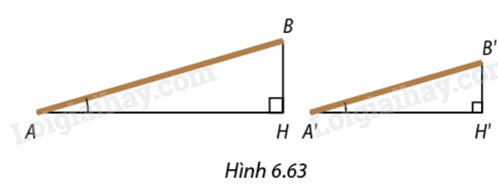
Bài 27 :

Trong Hình 6.63, hai đường ram dốc $AB$ và $A'B'$ có cùng tỉ số chiều cao và chiều dài $\frac{{BH}}{{AH}} = \frac{{B'H'}}{{A'H'}}.$ Em hãy giải thích vì sao $\widehat A = \widehat {A'}.$

Xem lời giải >>

Bài 28 :

Cho tam giác $ABC$ có $AH$ là đường cao và $A{H^2} = BH.CH$ . Chứng minh rằng:

a) Tam giác $ABC$ đồng dạng với tam giác $HBA$

b) Tam giác $ABC$ vuông tại A.

c) Cho $BH = \frac{5}{{13}}$ , Tính tỉ số chu vi và tỉ số diện tích của $\Delta ABH$ và $\Delta ABC$

Xem lời giải >>

Bài 29 :

Trong Hình 8, cho tam giác BEC $\left( BE<EC \right)$ . Cho biết $AC\bot BD,$ chứng minh rằng:

a) $\Delta AIB\backsim \Delta DIC$ .

b) $EA.EB=EC.ED$ .

Xem lời giải >>

Bài 30 :

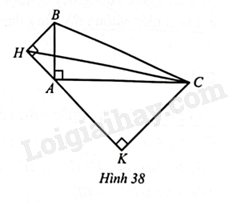
Hình 38 cho tam giác $ABC$ vuông ở $A$ , $AB = 5$ cm, $AC = 12$ cm. Tam giác $HAB$ vuông cân tại $H$ , tam giác $KAC$ vuông cân tại $K$ . Các cặp tam giác sau có đồng dạng với nhau không? Vì sao?

a) Tam giác $HAB$ và tam giác $KAC$ .

b) Tam giác $HKC$ và tam giác $BAC$ .

Xem lời giải >>