Đề bài

Cho tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với $4:5:6$ . Cho biết $\Delta ABC \backsim \Delta A'B'C'$ và cạnh nhỏ nhất của $\Delta A'B'C'$ bằng 2cm. Độ dài các cạnh còn lại của tam giác $A'B'C'$ lần lượt là

A.
3cm; 4cm
B.
2,5cm; 4cm.
C.
3cm; 2cm
D.
2,5cm; 3cm.

Phương pháp giải

Áp dụng tỉ số đồng dạng để tính độ dài của các cạnh.

Lời giải của GV HocTot.XYZ

Theo đầu bài tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với $4:5:6$

Và $\Delta ABC \backsim \Delta A'B'C'$ nên $\Delta A'B'C'$ cũng có độ dài các cạnh tỉ lệ với $4:5:6$

Giả sử $A'B' < A'C' < B'C' \Rightarrow A'B' = 2cm$

$\Rightarrow \frac{{A'B'}}{4} = \frac{{A'C'}}{5} = \frac{{B'C'}}{6} \Rightarrow \frac{{A'C'}}{5} = \frac{{B'C'}}{6} = \frac{2}{4}$

$\begin{array}{l} \Rightarrow A'C' = \frac{{5.2}}{4} = 2,5(cm)\\ \Rightarrow B'C' = \frac{{6.2}}{4} = 3(cm)\end{array}$

Độ dài các cạnh còn lại của tam giác A’B’C’ lần lượt là 2,5cm ; 3cm.

Đáp án : D

Báo lỗi - Góp ý

Các bài tập cùng chuyên đề

Bài 1 :

Trong các cặp tam giác sau cặp tam giác nào đồng dạng nếu các cạnh của hai tam giác có độ dài là :

A.
$3cm;4cm;6cm$ và $9cm;15cm;18cm$ .
B.
$4cm;5cm;6cm$ và $8cm;10cm;12cm$ .
C.
$6cm;5cm;6cm$ và $3cm;5cm;3cm$ .
D.
$5cm;7cm;1dm$ và $10cm;14cm;18cm$ .

Xem lời giải >>

Bài 2 :

Cho tam giác ABC có AB = 6cm; AC = 9cm; BC = 12cm và tam giác MNP có NP = 8cm; MN= 12cm; PM = 16cm. khẳng định nào sau đây là đúng?

A.
$\Delta ABC \backsim \Delta MNP$
B.
$\Delta ABC \backsim \Delta NMP$
C.
$\Delta ABC \backsim \Delta NPM$
D.
$\Delta BAC \backsim \Delta MNP$

Xem lời giải >>

Bài 3 :

Với điều kiện nào sau đây thì $\Delta ABC \backsim \Delta MNP$

A.
$\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}$ .
B.
$\frac{{AB}}{{MP}} = \frac{{AC}}{{MN}} = \frac{{BC}}{{NP}}$ .
C.
$\frac{{AB}}{{NP}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{MN}}$ .
D.
$\frac{{AB}}{{MN}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{MP}}$ .

Xem lời giải >>

Bài 4 :

Cho $\Delta ABC \backsim \Delta MNP$ biết $AB = 3cm;BC = 4cm;MN = 6cm;MP = 5cm$ . Khi đó:

A.
AC = 8cm; NP = 2,5cm
B.
AC = 2,5cm; NP = 8cm
C.
AC = 2,5cm; NP = 10cm
D.
AC = 10cm; NP = 2cm

Xem lời giải >>

Bài 5 :

Cho tam giác ABC có AB = 3cm, AC = 5cm; BC = 7cm và MNP có MN = 6cm;

MP = 10cm; NP = 14cm. Tỉ số chu vi của hai tam giác ABC và MNP là

A.
$\frac{3}{5}$ .
B.
2.
C.
$\frac{5}{6}$ .
D.
$\frac{1}{2}$ .

Xem lời giải >>

Bài 6 :

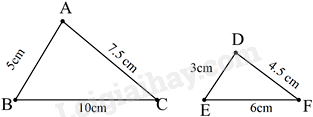
Cho hai tam giác ABC và DEF có kích thước như trong hình, hai tam giác có đồng dạng với nhau không, nếu có thì tỉ số đồng dạng là bao nhiêu?

A.
$\Delta ABC \backsim \Delta D{\rm{EF}}$ tỉ số đồng dạng là 2.
B.
Hai tam giác không đồng dạng.
C.
$\Delta ABC \backsim \Delta {\rm{FED}}$ tỉ số đồng dạng là $\frac{5}{3}$ .
D.
$\Delta ABC \backsim \Delta D{\rm{EF}}$ tỉ số đồng dạng là $\frac{5}{3}$ .

Xem lời giải >>

Bài 7 :

Cho hình vẽ sau, hãy cho biết hai tam giác nào đồng dạng?

A.
$\Delta ABC \backsim \Delta DBC$
B.
$\Delta A{\rm{D}}B \backsim \Delta DBC$
C.
$\Delta AB{\rm{D}} \backsim \Delta B{\rm{D}}C$
D.
$\Delta A{\rm{D}}C \backsim \Delta ABC$

Xem lời giải >>

Bài 8 :

Cho tam giác ABC có AB = 3cm; AC = 6cm; BC = 9cm và MNP có MN = 1cm; MP = 2cm; NP = 3cm. Tỉ số chu vi của hai tam giác MNP và ABC là

A.
$\frac{1}{2}$ .
B.
3.
C.
$\frac{1}{3}$ .
D.
2.

Xem lời giải >>

Bài 9 :

Cho tam giác ABC có AB = 12cm, AC = 8cm, BC = 6cm. Tam giác MNP đồng dạng với tam giác ABC và có chu vi bằng 52. Độ dài các cạnh của tam giác MNP là:

A.
MN = 12cm; MP = 16cm; NP = 24cm
B.
MN = 24cm; MP = 16cm; NP = 12cm
C.
MN = 16cm; MP = 24cm; NP = 12cm
D.
MN = 12cm; MP = 8cm; NP = 6cm

Xem lời giải >>

Bài 10 :

Cho $\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}$ khẳng định nào sau đây là sai

A.
$\frac{{AB}}{{{A_1}{B_1}}} = \frac{{AC}}{{{A_1}{C_1}}} = \frac{{BC}}{{{B_1}{C_1}}}$ .
B.
$\frac{{{A_1}{B_1}}}{{AB}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{B_1}{C_1}}}{{BC}}$ .
C.
$\frac{{{B_1}{C_1}}}{{BC}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{A_1}{B_1}}}{{AB}}$ .
D.
$\frac{{AB}}{{{A_1}{B_1}}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{BC}}{{{B_1}{C_1}}}$ .

Xem lời giải >>

Bài 11 :

Trong các cặp tam giác sau cặp tam giác nào đồng dạng nếu các cạnh của hai tam giác có độ dài là :

A.
1,5cm; 3cm; 4cm và 6cm; 12cm; 16cm.
B.
4cm; 5cm; 3cm và 8cm; 7dm; 6dm.
C.
6dm; 5dm; 4dm và 8dm; 7dm; 6dm.
D.
5cm; 7cm; 3 cm và 10cm; 14cm; 8cm.

Xem lời giải >>

Bài 12 :

Hai tam nào mà các cạnh có độ dài như sau thì không đồng dạng với nhau?

A.
4dm; 3dm; 2dm và 8 dm; 6dm; 4 dm.
B.
40cm; 50cm; 60cm và 7cm; 7cm; 5cm.
C.
14cm; 10cm ; 14cm và 7cm; 7cm; 5cm.
D.
9cm; 7cm; 3cm và 7cm; 14cm; 18cm.

Xem lời giải >>

Bài 13 :

Cho tam giác MNP có MN = 4cm; MP = 5cm; NP = 7cm và tam giác HIK có HI = 8cm; IK = 14cm; HK = 10cm. khẳng định nào sau đây là đúng:

A.
$\Delta MNP \backsim \Delta IHK$
B.
$\Delta MNP \backsim \Delta KIH$
C.

$\Delta HIK \backsim \Delta NPM$
D.

$\Delta MNP \backsim \Delta HIK$

Xem lời giải >>

Bài 14 :

Với điều kiện nào sau đây thì $\Delta MNP \backsim \Delta HIK$ ?

A.
$\frac{{HI}}{{NP}} = \frac{{HK}}{{MP}} = \frac{{IK}}{{MN}}$ .
B.
$\frac{{HI}}{{MN}} = \frac{{HK}}{{MP}} = \frac{{IK}}{{NP}}$ .
C.
$\frac{{HI}}{{NP}} = \frac{{HK}}{{MP}} = \frac{{IK}}{{MN}}$
D.
$\frac{{HI}}{{MP}} = \frac{{HK}}{{MN}} = \frac{{IK}}{{NP}}$

Xem lời giải >>

Bài 15 :

Lựa chọn đáp án đúng

Cho $\Delta HIK \backsim \Delta MNP$ biết HK = 3cm; HI = 4cm; MP = 9cm; NP = 12cm. Khi đó:

A.
MN = 8cm; IK = 6cm
B.
MN = 8cm; IK = 4cm
C.
MN = 12cm; IK = 4cm
D.
MN = 3cm; IK = 2cm

Xem lời giải >>

Bài 16 :

Cho tam giác ABC có AB= 16cm; AC = 18cm; BC = 25cm. Cho biết $\Delta ABC \backsim \Delta A'B'C'$ và AB – A’B’= 8cm. Độ dài các cạnh của tam giác A’B’C’ là:

A.
A’B’ = 8cm; A’C’ = 9cm; B’C’=12,5cm
B.
A’B’= 8cm; A’C’ = 9cm; B’C’ = 10cm
C.
A’B’= 10cm; A’C’ = 8cm; B’C’ = 12,5cm
D.
A’B’= 8cm; A’C’ = 12,5cm; B’C’ = 10cm

Xem lời giải >>

Bài 17 :

Tam giác thứ nhất có cạnh nhỏ nhất bằng 8cm, hai cạnh còn lại bằng x và y (x < y). Tam giác thứ hai có cạnh lớn nhất bằng 27cm hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đồng dạng:

A.
x = 12cm; y = 18cm
B.
x = 9cm; y = 24cm
C.
x = 18cm; y = 12cm
D.
x = 8cm; y = 27cm

Xem lời giải >>

Bài 18 :

Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Cho biết tam giác ABC có chu vi bằng 450cm, chu vi tam giác PQR có độ dài là

A.
220cm
B.
900cm
C.
225cm
D.
150cm

Xem lời giải >>

Bài 19 :

Những cặp tam giác nào dưới đây (hình 9.13) là đồng dạng? (các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.

Xem lời giải >>

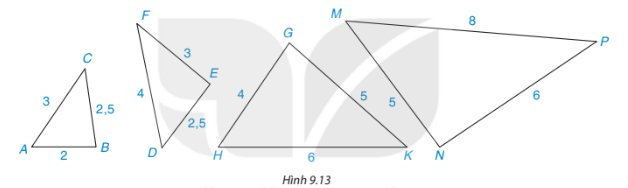
Bài 20 :

Cho tam giác ABC có chu vi bằng 18 cm và tam giác DEF có chu vi bằng 27cm. Biết rằng AB=4cm, BC=6cm, DE=6cm, FD=12cm. Chứng minh ΔABC ∽ ΔDEF

Xem lời giải >>

Bài 21 :

Trở lại tình huống mở đầu. Em hãy vẽ một tam giác có ba cạnh tỉ lệ với ba cạnh của tam giác tạo bởi ba đỉnh là trái bóng và hai chân cột gôn. Từ đó tính góc sút bằng góc tương ứng của tam giác vừa vẽ được.

Xem lời giải >>

Bài 22 :

Cho hai tam giác ABC và A'B'C' có độ dài các cạnh (theo đơn vị cm) như Hình 9.15. Biết rằng $\widehat A = \widehat {A'} = 60^0$

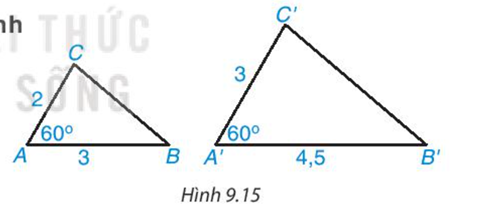
- So sánh các tỉ số $\frac{{A'B'}}{{AB}}{;^{}}\frac{{A'C'}}{{AC}}$

- Dùng thước có vạch chia đo độ dài BC, B'C' và tính tỉ số $\frac {B′C′} {BC}$

- Theo em, tam giác A'B'C' có đồng dạng với tam giác ABC không? Nếu có thì tỉ số đồng dạng là bao nhiêu?

Xem lời giải >>

Bài 23 :

Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4cm, 8cm và 10cm. Tam giác thứ hai có chu vi là 33cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?

a) 6cm, 12cm, 15cm

b) 8cm, 16cm, 20cm

c) 6cm, 9cm, 18cm

d) 8cm, 10cm, 15cm

Xem lời giải >>

Bài 24 :

Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA’B’C’ ∽ ΔABC

Chứng minh rằng $\frac{{A'M'}}{{AM}} = \frac{{B'N'}}{{BN}} = \frac{{C'P'}}{{CP}}$

Xem lời giải >>

Bài 25 :

Các trường hợp đồng dạng của hai tam giác có điều gì khác với các trường hợp bằng nhau của hai tam giác?

Xem lời giải >>

Bài 26 :

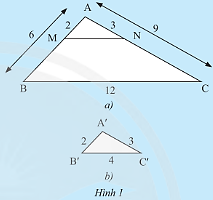
Cho tam giác $ABC$ và tam giác $A'B'C'$ có các kích thước như Hình 1. Trên cạnh $AB$ và $AC$ của tam giác $ABC$ lần lượt lấy hai điểm $M,N$ sao cho $AM = 2cm,AN = 3cm$ .

a) So sánh các tỉ số $\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}$ .

b) Tính độ dài đoạn thẳng $MN$ .

c) Em có nhận xét gì về mối liên hệ giữa các tam giác $ABC,AMN$ và $A'B'C'$ ?

Xem lời giải >>

Bài 27 :

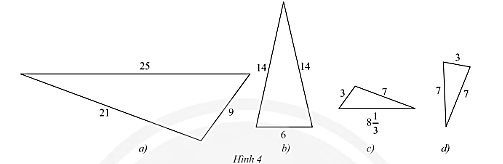
Tìm trong Hình 4 các cặp tam giác đồng dạng

Xem lời giải >>

Bài 28 :

a) Tam giác $AFE$ và $MNG$ ở Hình 14 có đồng dạng với nhau không? Vì sao?

b) Biết tam giác $AFE$ có chu vi bằng 15 cm. Tính chu vi tam giác MNG.

Xem lời giải >>

Bài 29 :

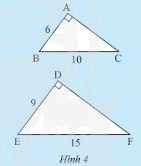
Cho hai tam giác vuông $ABC$ và $DEF$ có các kích thước như Hình 4.

a) Hãy tính độ dài cạnh $AC$ và $DF$ .

b) So sánh các tỉ số $\frac{{AB}}{{DE}};\frac{{AC}}{{DF}}$ và $\frac{{BC}}{{EF}}$ .

c) Dự đoán sự đồng dạng của hai tam giác $ABC$ và $DEF$ .

Xem lời giải >>

Bài 30 :

Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của AG, BG, CG. Chứng minh $\Delta A'B'C' \backsim\Delta ABC$ .

Xem lời giải >>

Cho tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với 4:5:64:5:6 . Cho biết ΔABC∽\Delta ABC \backsim \Delta A'B'C' và cạnh nhỏ nhất của \Delta A'B'C'\Delta A'B'C' bằng 2cm. Độ dài các cạnh còn lại của tam giác A'B'C'A'B'C' lần lượt là

Cho tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với $4:5:6$ . Cho biết $\Delta ABC \backsim \Delta A'B'C'$ và cạnh nhỏ nhất của $\Delta A'B'C'$ bằng 2cm. Độ dài các cạnh còn lại của tam giác $A'B'C'$ lần lượt là