Nội dung từ Loigiaihay.Com
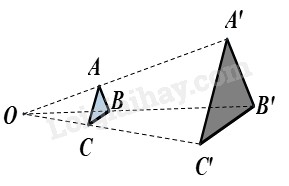
Cho hai tam giác ABC và A’B’C’ sao cho 3 đường thẳng AA’, BB’, CC’ cùng đi qua điểm O và \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3.\) Khi đó, tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là:
-
A.
3
-
B.
\(\frac{1}{3}\)
-
C.
\(2\)
-
D.
\(\frac{1}{2}\)
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
+ Nếu \(k > 1\) thì ta nói \(\mathcal{K}'\) là hình phóng to của hình \(\mathcal{K}\), nếu \(k < 1\) thì ta nói \(\mathcal{K}'\) là hình thu nhỏ của hình \(\mathcal{K}\)
Vì \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 3\) nên tam giác A’B’C’ và tam giác ABC là đồng dạng phối cảnh với tỉ số vị tự là 3.
Do đó tam giác ABC và tam giác A’B’C’ là đồng dạng phối cảnh với tỉ số vị tự là \(\frac{1}{3}\).
Đáp án : B

Các bài tập cùng chuyên đề












