Nội dung từ Loigiaihay.Com
Đề bài
Cho tam giác ABC có \(AB = 2,BC = 3,CA = 4\) , AD là đường phân giác và I là giao điểm của ba đường phân giác của tam giác đó. Tính tỉ số \(\frac{{ID}}{{IA}}\)
-
A.
\(\frac{5}{6}\)
-
B.
\(\frac{1}{3}\)
-
C.
\(\frac{1}{2}\)
-
D.
\(\frac{3}{4}\)
Phương pháp giải
Sử dụng kiến thức về tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Lời giải của GV HocTot.XYZ
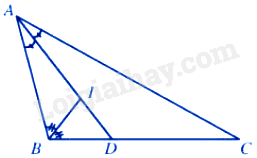
Trong tam giác ABC có AD là đường phân giác của góc BAC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} = \frac{2}{4} = \frac{1}{2}\) nên \(\frac{{DB}}{1} = \frac{{DC}}{2}\)
Theo tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{DB}}{1} = \frac{{DC}}{2} = \frac{{DB + DC}}{{1 + 2}} = \frac{{BC}}{3} = \frac{3}{3} = 1\)
Do đó, \(DB = 1\)
Xét tam giác ABD có BI là đường phân giác của góc ABD nên \(\frac{{ID}}{{IA}} = \frac{{BD}}{{BA}} = \frac{1}{2}\)
Đáp án : C

Các bài tập cùng chuyên đề












