Nội dung từ Loigiaihay.Com
Đề bài
Cho tam giác ABC có AM là đường trung tuyến. Gọi MD, ME lần lượt là đường phân giác của các tam giác AMB và AMC. Gọi I là giao điểm của DE và AM.
Chọn đáp án đúng.
-
A.
\(DI = \frac{4}{5}IE\)
-
B.
\(DI = \frac{3}{4}IE\)
-
C.
\(DI = \frac{2}{3}IE\)
-
D.
\(DI = IE\)
Phương pháp giải
Sử dụng kiến thức về tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Lời giải của GV HocTot.XYZ
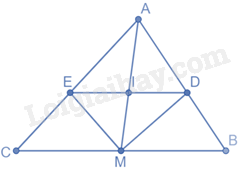
Xét tam giác AMB có MD là đường phân giác của góc AMB nên \(\frac{{DA}}{{DB}} = \frac{{MA}}{{MB}}\)
Xét tam giác AMC có ME là đường phân giác của góc AMC nên \(\frac{{EA}}{{EC}} = \frac{{MA}}{{MC}}\)
Mà \(MB = MC\) nên \(\frac{{MA}}{{AB}} = \frac{{MA}}{{MC}}\) nên \(\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}}\) , do đó DE//BC (định lý Thalès đảo)
Áp dụng hệ quả của định lý Thalès vào hai tam giác ABM và ACM có:
\(\frac{{ID}}{{MB}} = \frac{{IA}}{{AM}}\) và \(\frac{{IE}}{{MC}} = \frac{{AI}}{{AM}}\) , do đó, \(\frac{{ID}}{{MB}} = \frac{{IE}}{{MC}}\)
Mà \(MB = MC\) nên \(DI = IE\)
Đáp án : D
Các bài tập cùng chuyên đề