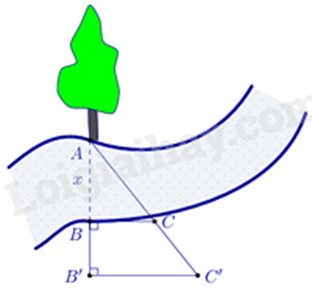
Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng của một khúc sông mà không cần phải sang bờ bên kia sông (hình vẽ bên). Biết \(BB' = 20\) m, \(BC = 30\) m và \(B'C' = 40\) m. Tính độ rộng \(x\) của khúc sông.

Bài 1 :

Cho điểm \(M\) thuộc đoạn thẳng \(AB\) sao cho \(MA = 2MB\) . Vẽ về một phía của \(AB\) các tam giác đều \(AMC\) và \(MBD\) . Gọi \(E\) là giao điểm của \(AD\) và \(MC\) , \(F\) là giao điểm của \(BC\) và \(DM\) . Đặt \(MB = a\) . Tính \(ME,MF\) theo \(a\) .

Bài 2 :

Cho tứ giác \(ABCD\) . Qua \(E \in AD\) kẻ đường thẳng song song với \(DC\) cắt \(AC\) ở \(G\) . Qua \(G\) kẻ đường thẳng song song với \(CB\) cắt \(AB\) tại \(H\) . Qua \(B\) kẻ đường thẳng song song với \(CD\) , cắt đường thẳng \(AC\) tại \(I\) . Qua \(C\) kẻ đường thẳng song song với \(BA\) , cắt \(BD\) tại \(F\) . Khẳng định nào sau đây là sai?

Bài 3 :

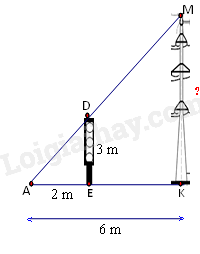
Bóng \(\left( {AK} \right)\) của một cột điện \(\left( {MK} \right)\) trên mặt đất dài 6m. Cùng lúc đó một cột đèn giao thông \(\left( {DE} \right)\) cao 3m có bóng \(\left( {AE} \right)\) dài 2m. Tính chiều cao của cột điện \(\left( {MK} \right)\) .

Bài 4 :

Để đo chiều cao \(AC\) của một cột cờ, người ta cắm một cái cọc \(ED\) có chiều cao 2m vuông góc với mặt đất. Đặt vị trí quan sát tại \(B\) , biết khoảng cách \(BE\) là 1,5m và khoảng cách \(AB\) là 9m.

Tính chiều cao \(AC\) của cột cờ.

Bài 5 :

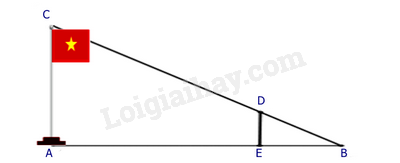
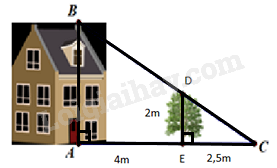
Tính chiều cao \(AB\) của ngôi nhà biết cái cây có chiều cao \(ED = 2\) m và khoảng cách \(AE = 4\) m, \(EC = 2,5\) m.

Bài 6 :

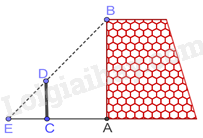
Một nhóm các bạn học sinh lớp 8 đã thực hành đo chiều cao \(AB\) của một bức tường như sau: Dùng một cái cọc \(CD\) đặt cố định vuông góc với mặt đất, với \(CD = 3\) m và \(CA = 5\) m. Sau đó, các bạn đã phối hợp để tìm được điểm \(E\) trên mặt đất là giao điểm của hai tia \(BD,\,AC\) và đo được \(CE = 2,5\) m (Hình vẽ bên). Tính chiều cao \(AB\) của bức tường.

Bài 7 :

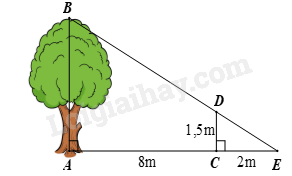
Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao 1,5m so với mặt đất, chân cọc cách gốc cây 8m và cách bóng của đỉnh cọc 2m. Tính chiều cao của cây. (Kết quả làm tròn đến chữ số thập phân thứ nhất).

Bài 8 :

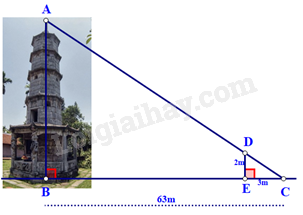
Bóng của một tháp trên mặt đất có độ dài \(BC = 63\) m. Cùng thời điểm đó, một cây cột \(DE\) cao 2 mét cắm vuông góc với mặt đất có bóng dài 3 mét. Tính chiều cao của tháp?

Bài 9 :

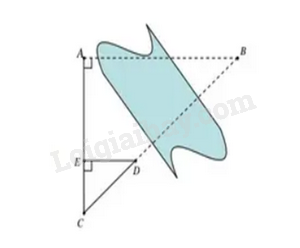
Để đo khoảng cách giữa hai điểm \(A\) và \(B\) (không thể đo trực tiếp), người ta xác định các điểm \(C,\,D,\,E\) như hình vẽ. Sau đó đo được khoảng cách giữa \(A\) và \(C\) là \(AC = 6\) m, khoảng cách giữa \(C\) và \(E\) là \(EC = 2\) m; khoảng cách giữa \(E\) và \(D\) là \(DE = 3\) m. Tính khoảng cách giữa hai điểm \(A\) và \(B\) .

Bài 10 :

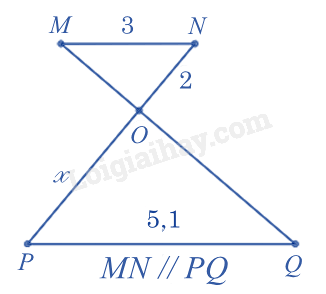
Cho hình vẽ sau, biết MN // PQ, số đo cạnh OP là:

Bài 11 :

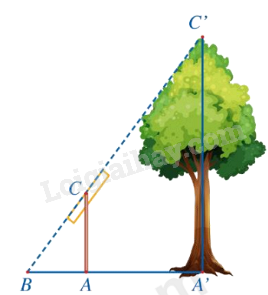
Trong hình dưới đây, độ dài đoạn thẳng \({\rm{A'C'}}\) mô tả chiều cao của một cái cây, đoạn thẳng \({\rm{AC}}\) mô tả chiều cao của một cái cọc (cây và cọc cùng vuông góc với đường thẳng đi qua ba điểm \(\left. {A',A,B} \right)\). Giả sử \(AC = 2{\rm{\;m}},AB = 1,5{\rm{\;m}},A'B = 4,5{\rm{\;m}}\). Tính chiều cao của cây.

Bài 12 :

Cho tam giác ABC, đường thẳng d song song với BC cắt 2 cạnh AB và AC lần lượt tại M và N. Biết rằng \(\frac{{AM}}{{MB}} = \frac{1}{2}.\) Tính tỉ số chu vi tam giác AMN và ABC?

A. \(\frac{1}{3}.\)

B. \(\frac{2}{3}.\)

C. \(\frac{1}{2}.\)

D. \(\frac{1}{4}.\)

Bài 13 :

Tìm độ dài \(x\) trên Hình 13.

Bài 14 :

Với số liệu đo đạc được ghi trên Hình 14, hãy tính bề rộng \(CD\) của con kênh.

Bài 15 :

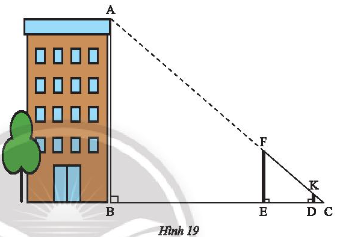
Đo chiều cao \(AB\) của một tòa nhà bằng hai cây cọc \(FE,DK\), một sợi dây và một thước cuộn như sau:

- Đặt cọc \(FE\) cố định, di chuyển cọc \(DK\) sao cho nhìn thấy \(K,F,A\) thẳng hàng.

- Căng thẳng dây \(FC\) đi qua \(K\) và cắt mặt đất tại \(C\).

- Đo khoảng cách \(BC\) và \(DC\) trên mặt đất.

Cho biết \(DK = 1m,BC = 24m,DC = 1,2m\). Tính chiều cao \(AB\) của tòa nhà.

Bài 16 :

Với số liệu được ghi trên Hình 21. Hãy tính khoảng cách \(CD\) từ con tàu đến trạm quan trắc đặt tại điểm \(C\).

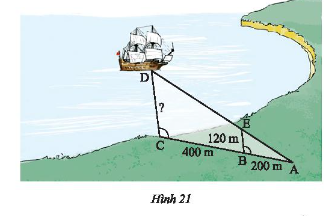
Bài 17 :

Tính các độ dài \(x,y\) trong Hình 23.

Bài 18 :

Cho hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Chứng minh rằng \(OA.OD = OB.OC\)

Bài 19 :

Quan sát Hình 25 và chứng minh: \(x = \frac{{ah}}{{a' - a}}\).

Bài 20 :

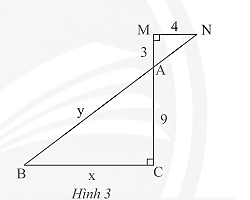
Cho Hình 3, biết \(AM = 3cm;MN = 4cm;AC = 9cm.\) Giá trị của biểu thức \(x - y\) là

A. 4.

B. -3.

C. 3.

D. -4

Bài 21 :

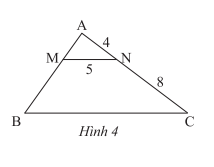
Cho Hình 4, biết \(MN//BC,AN = 4cm,NC = 8cm,MN = 5cm.\) Độ dài cạnh \(BC\)

A. 10cm.

B. 20cm.  

C. 15cm.

D. 16cm.

Bài 22 :

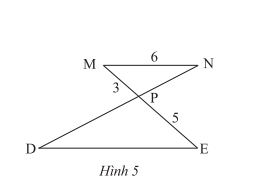
Cho Hình 5, biết \(MN//DE,MN = 6cm;MP = 3cm;PE = 5cm\). Độ dài đoạn thẳng \(DE\) là

A. 6cm.

B. 5cm.

C. 8cm.

D. 10cm.

Bài 23 :

Cho tam giác \(ABC\) và điểm \(D\) trên cạnh \(AB\) sao cho \(AD = 13,5cm;DB = 4,5cm\). Tính tỉ số các khoảng cách từ điểm \(D\) và \(B\) đến đoạn thẳng \(AC\).

Bài 24 :

Cho tam giác ABC có \(AB = 4,5cm,\,\,AC = 6cm\). Các điểm M, N lần lượt thuộc các cạnh AB, AC thỏa mãn \(AM = 3cm\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng AN.

Bài 25 :

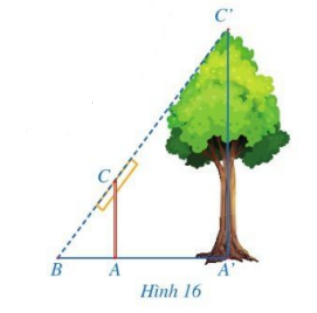
Trong Hình 16, độ dài đoạn thẳng A’C’ mô tả chiều cao của một cái cây, đoạn thẳng AC mô tả một cái cọc (cây và cọc cùng vuông góc với đường thẳng đi qua ba điểm A’, A, B). Giả sử \(AC = 2m,\,\,AB = 1,5m,\,\,A'B = 4,5m\). Tính chiều cao của cây.

Bài 26 :

Cho đoạn thẳng AB. Hãy trình bày cách chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau mà không cần dùng thước đo.

Bài 27 :

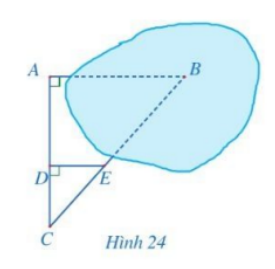
Để đo khoảng cách giữa hai vị trí A và B trong đó B không tới được, người ta tiến hành chọn các vị trí C, D, E như ở Hình 24 và đo được \(AC = 50m,\,\,CD = 20m,\,\,DE = 18m\). Hỏi khoảng cách giữa hai vị trí A và B là bao nhiêu?

Bài 28 :

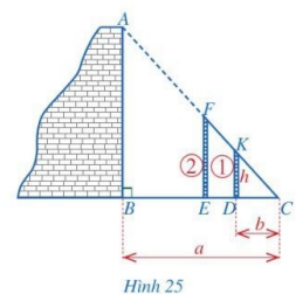
Có thể gián tiếp đo chiều cao của một bức tường khá cao bằng dụng cụ đơn giản được không?

Hình 25 thể hiện cách đo chiều cao AB của một bức tường bằng các dụng cụ đơn giản gồm: Hai cọc thẳng đứng (Cọc 1 cố định; cọc 2 có thể di động được) và sợi dây FC. Cọc 1 có chiều cao \(DK = h\). Các khoảng cách \(BC = a,\,\,DC = b\) đo được bằng thước dây thông dụng.

a)      Em hãy cho biết người ta tiến hành đo đạc như thế nào?

b)     Tính chiều cao AB theo \(h,\,\,a,\,\,b\).

Bài 29 :

Anh Thiện và chị Lương đứng ở hai phía bờ song và muốn ước lượng khoảng cách giữa hai vị trí A, B ở hai bên bờ sông (Hình 27).

-         Anh Thiện chọn vị trí C ở bên bờ sông sao cho A, B, C thẳng hàng và đo được BC=4m;

-         Tiếp theo, anh Thiện xác định vị trí D, chị Lương xác định vị trí E sao cho D, B, E thẳng hàng, đồng thời \(\widehat {BAE} = \widehat {BCD} = 90^\circ \);

-         Anh Thiện đo được CD=2m, chị Lương đo được AE=12m.

-         Hãy tính khoảng cách giữa hai vị trí A và B.

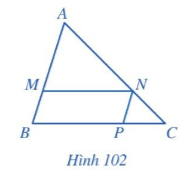
Bài 30 :

Cho tam giác ABC, các điểm M, N, P lần lượt thuộc các cạnh AB, AC, BC sao cho tứ giác BMNP là hình bình hành (Hình 102). Chứng minh \(\frac{{MN}}{{BC}} + \frac{{NP}}{{AB}} = 1\).