Nội dung từ Loigiaihay.Com
Đề bài
Hàm số $y = {x^3} - 3x^2 + 4$ đạt cực tiểu tại:
-
A.
$x = 0$
-
B.
$x = 2$
-
C.
$x = 4$
-
D.
$x = 0$ và $x = 2$
Phương pháp giải
Quy tắc 1:
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tính $f'\left( x \right)$, tìm các điểm tại đó $f'\left( x \right) = 0$ hoặc không xác định.
- Bước 3: Lập bảng biến thiên và kết luận.
+ Tại các điểm mà đạo hàm đổi dấu từ âm sang dương thì đó là điểm cực tiểu của hàm số.
+ Tại các điểm mà đạo hàm đổi dấu từ dương sang âm thì đó là điểm cực đại của hàm số.
Lời giải của GV HocTot.XYZ
TXĐ: $D=R$
Ta có: $y' = 3{x^2} - 6x$
$ \Rightarrow y' = 0 \Leftrightarrow x = 0$ hoặc $x = 2$
Ta có bảng biến thiên:
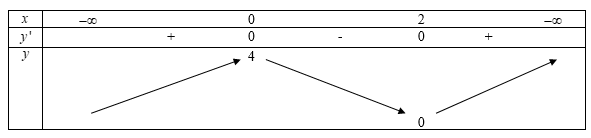
Từ bảng dễ thấy hàm số đạt giá trị cực tiểu $y = 0$ tại $x = 2$
Đáp án : B
Chú ý
HS thường nhầm điểm $x = 0$ là điểm cực tiểu của hàm số vì thấy $0 < 2$.

Các bài tập cùng chuyên đề












