Nội dung từ Loigiaihay.Com
Đề bài
Cho tam giác ABC và một điểm S không thuộc mặt phẳng ABC. Gọi M, N lần lượt là trung điểm của AB và AC. Khi đó, giao tuyến của hai mặt phẳng (SBN) và (SCM) là:
-
A.
SG với G là giao điểm của BN và MC.
-
B.
SN.
-
C.
SM.
-
D.
AG với G là giao điểm của BN và MC.
Phương pháp giải
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Đường thẳng chung d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó.
Lời giải của GV HocTot.XYZ
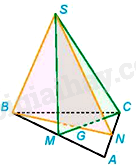
Xét mặt phẳng (ABC), gọi G là giao điểm của BN và CM.
Vì \(G \in BN \Rightarrow G \in \left( {SBN} \right);G \in CM \Rightarrow G \in \left( {SCM} \right)\) nên G là điểm chung của hai mặt phẳng (SBN) và (SCM)
Ta có: \(S \in SB \Rightarrow S \in \left( {SBN} \right),S \in SC \Rightarrow S \in \left( {SCM} \right)\) nên S là điểm chung của hai mặt phẳng (SBN) và (SCM)
Do đó, SG là giao tuyến của hai mặt phẳng (SBN) và (SCM).
Đáp án : A
Các bài tập cùng chuyên đề