Cho $\Delta ABC$ có $AB < BC$. Trên tia BA lấy điểm D sao cho $BC = BD$. Tia phân giác $\widehat B$ cắt AC ở E. Gọi K là trung điểm của DC.

a) Chứng minh $\Delta BED = \Delta BEC$.

b) Chứng minh $EK \bot DC$.

c) Chứng minh B, K, E thẳng hàng.

d) Kẻ $AH \bot DC,\left( {H \in DC} \right)$. $\Delta ABC$ cần thêm điều kiện gì để $\widehat {DAH} = {45^0}$.

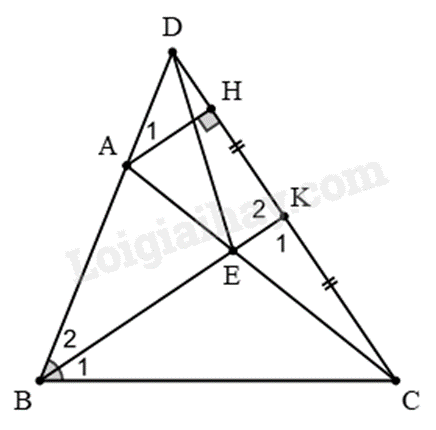
a) Xét $\Delta BED$ và $\Delta BEC$ có:

BD = BC (gt)

$\widehat {{B_2}} = \widehat {{B_1}}$ (BE là tia phân giác của $\widehat {ABC}$)

BE chung

$\Rightarrow \Delta BED = \Delta BEC$(c.g.c) (đpcm)

$\Rightarrow DE = EC$ (hai cạnh tương ứng)

b) Xét $\Delta EKD$ và $\Delta EKC$ có:

ED = EC (cmt)

EK chung

DK = KC (K là trung điểm của DC)

$\Rightarrow \Delta EKD = \Delta EKC$(c.c.c)

$\Rightarrow \widehat {{K_1}} = \widehat {{K_2}}$(hai cặp góc tương ứng)

Mà $\widehat {{K_1}}$ và $\widehat {{K_2}}$ là hai góc kề bù nên $\widehat {{K_1}} = \widehat {{K_2}} = \frac{{{{180}^0}}}{2} = {90^0}$ hay $EK \bot DC$. (1) (đpcm)

c) Xét $\Delta BKD$ và $\Delta BKC$ có:

BD = BC (gt)

BK chung

DK = KC (K là trung điểm của DC)

$\Rightarrow \Delta BKD = \Delta BKC$(c.c.c)

$\Rightarrow \widehat {BKD} = \widehat {BKC}$(hai cặp góc tương ứng)

Mà $\widehat {BKD}$ và $\widehat {BKC}$ là hai góc kề bù nên $\widehat {BKD} = \widehat {BKC} = \frac{{{{180}^0}}}{2} = {90^0}$ hay $BK \bot DC$ (2)

Từ (1) và (2) suy ra B, E, K thẳng hàng. (đpcm)

d) Ta có: $AH \bot DC$; $BK \bot DC \Rightarrow AH//BK$

$\Rightarrow \widehat {{A_1}} = \widehat {{B_2}}$ (hai góc đồng vị).

Để $\widehat {{A_1}} = {45^0}$ thì $\widehat {{B_2}} = {45^0}$, mà $\widehat {{B_2}} = \widehat {{B_1}} = \frac{1}{2}\widehat {ABC}$ nên $\widehat {ABC} = {45^0}.2 = {90^0}$ hay tam giác ABC vuông tại B.

Vậy tam giác ABC tam giác cân tại B thì ta có $\widehat {DAH} = {45^0}$.