Nội dung từ Loigiaihay.Com
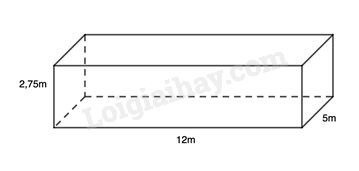
Một bể bơi dạng hình hộp chữ nhật có chiều dài 12m, chiều rộng 5m và sâu 2,75m như hình vẽ.
a) Tính diện tích xung quanh thành bể và diện tích đáy của bể bơi.
b) Hỏi người thợ phải dùng bao nhiêu viên gạch men để lát đáy và xung quanh thành bể đó? Biết rằng mỗi viên gạch có chiều dài 25cm, chiều rộng 20 cm và diện tích mạch vữa lát không đáng kể.
a) Sử dụng công thức tính diện tích xung quanh hình hộp chữ nhật: Sxq = chu vi đáy.chiều cao.
Sử dụng công thức tính diện tích hình chữ nhật để tính diện tích đáy bể bơi.
b) Tổng diện tích xung quanh và diện tích đáy bể chính là diện tích cần lát gạch.
Tính diện tích mỗi viên gạch.
Số viên gạch bằng diện tích cần lát : diện tích mỗi viên gạch.
a) Diện tích xung quanh thành bể:
\(\left[ {(12 + 5).2} \right].2,75 = 93,5\,{m^2}\)
Diện tích đáy bể:
\(12.5 = 60\,{m^2}\)
b) Diện tích cần lát gạch:
\(93,5 + 60 = 153,5\,{m^2}\)
Diện tích mỗi viên gạch:
\(0,25.0,2 = 0,05\,{m^2}\)
Số viên gạch cần lát là: \(153,5:0,05 = 3070\)(viên).
Vậy cần dùng 3070 viên gạch để lát.

Các bài tập cùng chuyên đề












