Nội dung từ Loigiaihay.Com
Đề bài
Cho hình hộp ABCD.A’B’C’D’ có \(AA' \bot \left( {ABCD} \right)\). Khẳng định nào dưới đây đúng?
-
A.
(ABCD)\( \bot \) (A’B’C’D).
-
B.
\(BB' \bot \left( {ABCD} \right)\).
-
C.
Cả A và B đều đúng.
-
D.
Cả A và B đều sai.
Phương pháp giải
Cho hai đường thẳng song song, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Lời giải của GV HocTot.XYZ
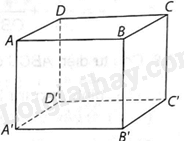
Vì \(AA' \bot \left( {ABCD} \right)\) và AA’//BB’ nên \(BB' \bot \left( {ABCD} \right)\)
Đáp án B.
Đáp án : B

Các bài tập cùng chuyên đề












