Nội dung từ Loigiaihay.Com
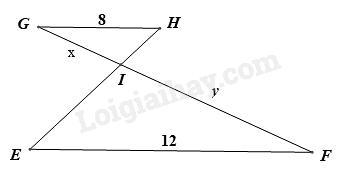
Cho $\Delta GHI\backsim \Delta FEI$ có các kính thước như hình vẽ, khi đó tỉ số độ dài của y và x bằng:
-
A.
\(4\).
-
B.
\(\frac{2}{3}\).
-
C.
\(\frac{3}{2}\).
-
D.
\(6\).
Từ hai tam giác đồng dạng suy ra tỉ số đồng dạng
Vì $\Delta GHI\backsim \Delta FEI$ nên \(\frac{y}{x} = \frac{{IF}}{{GI}} = \frac{{EF}}{{GH}} = \frac{{12}}{8} = \frac{3}{2}\).
Đáp án C.
Đáp án : C

Các bài tập cùng chuyên đề
Bài 1 :
Hãy chọn câu đúng.
-
A.
Hai tam giác bằng nhau thì đồng dạng.
-
B.
Hai tam giác đồng dạng thì bằng nhau.
-
C.
Hai tam giác bằng nhau thì không đồng dạng.
-
D.
Hai tam giác vuông luôn đồng dạng với nhau.
Bài 2 :
Hãy chọn câu sai.
-
A.
Hai tam giác bằng nhau thì đồng dạng.
-
B.
Hai tam giác đều luôn đồng dạng.
-
C.
Hai tam giác cân thì đồng dạng.
-
D.
Hai tam giác đồng dạng là hai tam giác có tất cả các cặp góc tương ứng bằng nhau và các cặp cạnh tương ứng tỉ lệ.
Bài 3 :
Cho \(\Delta ABC,\Delta MNP\) nếu có \(\widehat A = \widehat M;\widehat B = \widehat N;\widehat C = \widehat P\) để \(\Delta ABC \backsim \Delta MNP\) theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?
-
A.
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) .
-
B.
\(\frac{{AB}}{{NP}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NM}}\) .
-
C.
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{MP}}\) .
-
D.
\(\frac{{AB}}{{MP}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{NM}}\) .
Bài 4 :
Cho \(\Delta ABC \backsim \Delta MNP\) theo tỉ số 2. Khẳng định nào sau đây là đúng
-
A.
\(MN = 2{\rm{A}}B\) .
-
B.
\(AC = 2NP\) .
-
C.
\(MP = 2BC\) .
-
D.
\(BC = 2.NP\) .
Bài 5 :
Hãy chọn câu đúng
Nếu \(\Delta ABC \backsim \Delta MNP\) theo tỉ số \(k = \frac{2}{3}\) thì \(\Delta MNP \backsim \Delta ABC\) theo tỉ số
-
A.
\(\frac{2}{3}\) .
-
B.
\(\frac{3}{2}\) .
-
C.
\(\frac{4}{9}\) .
-
D.
\(\frac{4}{3}\) .
Bài 6 :
Cho \(\Delta ABC,\Delta MNP\) biết \(AB = 3cm;AC = 4cm;BC = 5cm;MN = 6cm;MP = 8cm;NP = 10cm\) và \(\widehat A = {90^o};\widehat B = {60^o};\widehat M = {90^o};\widehat P = {30^o}\) thì:
-
A.
\(\Delta ABC \backsim \Delta PNM\) .
-
B.
\(\Delta ABC \backsim \Delta NMP\) .
-
C.
\(\Delta ABC \backsim \Delta MNP\) .
-
D.
\(\Delta ABC \backsim \Delta MPN\) .
Bài 7 :
Cho \(\Delta ABC \backsim \Delta D{\rm{EF}}\) biết \(\widehat A = {50^o};\widehat B = {60^o}\) . Khi đó số đo góc D bằng
-
A.
\({50^o}\) .
-
B.
\({60^o}\) .
-
C.
\({70^o}\) .
-
D.
\({80^o}\) .
Bài 8 :
Cho tam giác ABC, trên AB lấy điểm D. Qua D kẻ đường thẳng song song với BC cắt AC ở E. Khẳng định nào sau đâyđúng
-
A.
\(\Delta ABC \backsim \Delta A{\rm{D}}E\) .
-
B.
\(\Delta ABC \backsim \Delta A{\rm{ED}}\) .
-
C.
\(\Delta BAC \backsim \Delta A{\rm{D}}E\) .
-
D.
\(\Delta ACB \backsim \Delta DE{\rm{A}}\) .
Bài 9 :
Cho \(\Delta ABC \backsim \Delta DEF\) theo tỉ số \({k_1}\) , \(\Delta MNP \backsim \Delta D{\rm{EF}}\) theo tỉ số \({k_2}\) . Hỏi \(\Delta ABC \backsim \Delta MNP\) theo tỉ số nào ?
-
A.
\({k_1}\) .
-
B.
\(\frac{{{k_2}}}{{{k_1}}}\) .
-
C.
\(\frac{{{k_1}}}{{{k_2}}}\) .
-
D.
\({k_1}{k_2}\) .
Bài 10 :
Cho \(\Delta ABC \backsim \Delta MNP\) . Biết \(AB = 5cm;BC = 6cm;MN = 10cm;MP = 5cm\) . Hãy chọn đáp án đúng:
-
A.
\(NP = 2,5cm;AC = 12cm\)
-
B.
\(NP = 12cm;AC = 2,5cm\)
-
C.
\(NP = 5cm;AC = 10cm\)
-
D.
\(NP = 10cm;AC = 5cm\)
Bài 11 :
Cho \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) theo tỉ số \(2:3\) và \(\Delta {A_1}{B_1}{C_1} \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số 1 :3. Vậy \(\Delta ABC \backsim \Delta {A_2}{B_2}{C_2}\) theo tỉ số k bằng
-
A.
\(k = 3:9\)
-
B.
\(k = 2:9\)
-
C.
\(k = 2:6\)
-
D.
\(k = 1:3\)
Bài 12 :
Cho \(\Delta {A_1}{B_1}{C_1} \backsim \Delta ABC\) theo tỉ số đồng dạng \(k = \frac{2}{3}\) . Tỉ số chu vi của hai tam giác đó là:
-
A.
\(\frac{4}{9}\).
-
B.
\(\frac{3}{2}\).
-
C.
\(\frac{3}{4}\).
-
D.
\(\frac{2}{3}\).
Bài 13 :
Nếu \(\Delta {A_1}{B_1}{C_1}\) đồng dạng với \(\Delta ABC\) theo tỉ số 4 thì tỉ số chu vi của \(\Delta {A_1}{B_1}{C_1}\) và \(\Delta ABC\) là
-
A.
4
-
B.
16
-
C.
8
-
D.
0,25
Bài 14 :
\(\Delta ABC \backsim \Delta D{\rm{EF}}\) theo tỉ số \(k = \frac{3}{2}\) , biết \(\Delta ABC\) có chu vi bằng 42cm. Chu vi \(\Delta D{\rm{EF}}\) là:
-
A.
28cm
-
B.
2cm
-
C.
8cm
-
D.
18cm
Bài 15 :
Cho \(\Delta MNI \backsim \Delta ABC\) theo tỉ số \(k = \frac{5}{7}\) và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.
-
A.
\({C_{\Delta MNI}} = 30m,{C_{\Delta ABC}} = 46m.\)
-
B.
\({C_{\Delta MNI}} = 56m,{C_{\Delta ABC}} = 40m.\)
-
C.
\({C_{\Delta MNI}} = 24m,{C_{\Delta ABC}} = 40m.\)
-
D.
\({C_{\Delta MNI}} = 40m,{C_{\Delta ABC}} = 56m.\)
Bài 16 :
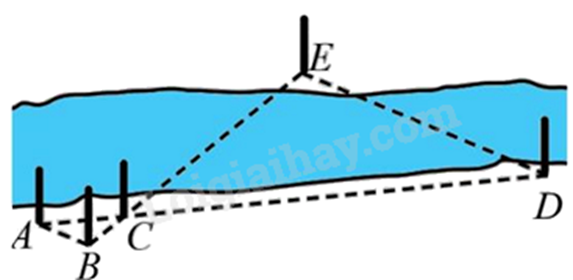
Để đo khoảng cách giữa hai địa điểm \({\rm{D}}\), \({\rm{E}}\) ở hai bên bờ của một con sông, người ta chọn các vị trí \({\rm{A}}, {\rm{B}}, {\rm{C}}\) ở cùng một bên bờ với điểm \(D\) và đo được \(AB = 2{\rm{\;m}},AC = 3{\rm{\;m}},CD = 15{\rm{\;m}}\). Giả sử $\Delta ABC\backsim \Delta DEC$. Tính khoảng cách \(DE\).
-
A.
\(10{\rm{\;m}}\)
-
B.
\(12{\rm{\;m}}\)
-
C.
\(9{\rm{\;m}}\)
-
D.
\(15{\rm{\;m}}\)
Bài 17 :
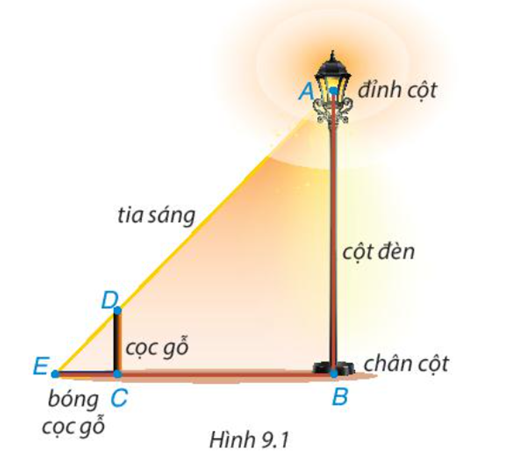
Có một chiếc bóng điện được mắc trên đỉnh (Điểm A) của cột đèn thẳng đứng. Để tính chiều cao AB của cột đèn, bác Dương cắm một chiếc cọc gỗ (đoạn CD) thẳng đứng trên mặt đất rồi đo chiều dài bóng của cọc gỗ do ánh đèn điện tạo ra và đo khoảng cách từ điểm E đến chân cột đèn (điểm B). Theo em bác Dương đã tính như thế nào để ra được chiều cao cột đèn?
Bài 18 :
Trong hình 9.2, ΔABC và ΔDEF là hai tam giác có các cạnh tương ứng song song và các góc tương ứng bằng nhau, tức là AB // DE, AC // DF, BC // EF và \(\widehat A = \widehat D{,^{}}\widehat B = \widehat E{;^{}}\widehat C = \widehat F\)

Nhìn hình vẽ, hãy cho biết giá trị các tỉ số sau: \(\frac{{AB}}{{DE}}{;^{}}\frac{{BC}}{{EF}}{;^{}}\frac{{AC}}{{DF}}\)
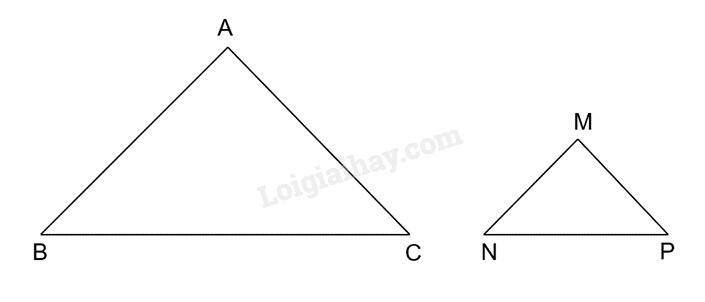
Bài 19 :
Trong các tam giác được vẽ trên ô lưới vuông, có một cặp tam giác đồng dạng. Hãy chỉ ra cặp tam giác đó, viết đúng kí hiệu đồng dạng và tìm tỉ số đồng dạng của chúng.

Bài 20 :
Cho \(\Delta ABC \backsim \Delta MNP\). Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì tam giác MNP cân tại đỉnh M.
b) Nếu tam giác ABC đều thì tam giác MNP đều.
c) Nếu \(AB \ge AC \ge BC\) thì \(MN \ge MP \ge NP\)
Bài 21 :
Cho ΔABC \(\backsim\) ΔMNP, khẳng định nào sau đây không đúng?
a) ΔMNP \(\backsim\) ΔABC
b) ΔBCA \(\backsim\) ΔNPM
c) ΔCAB \(\backsim\) ΔPNM
d) ΔACB \(\backsim\) ΔMNP
Bài 22 :
Khẳng định nào sau đây là đúng?
a) Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Hai tam giác bất kì đồng dạng với nhau
c) Hai tam giác đều bất kì đồng dạng với nhau
d) Hai tam giác vuông bất kì đồng dạng với nhau
e) Hai tam giác đồng dạng thì bằng nhau
Bài 23 :
Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng \(\widehat {BAC} = \widehat {PMN}\), AB=2MN. Chứng minh ΔMNP ∽ ΔABC và tìm tỉ số đồng dạng
Bài 24 :
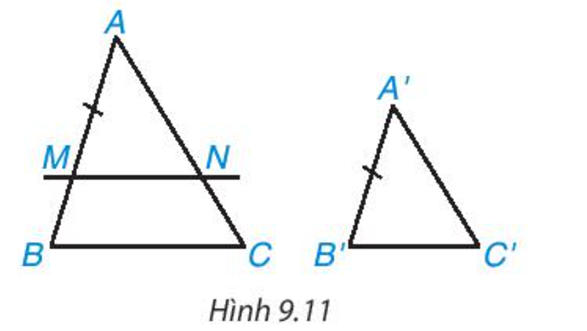
Cho hai tam giác ABC và A'B'C' có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
a) Nếu A′B=AB thì hai tam giác có đồng dạng với nhau không? Vì sao?
b) Nếu A′B < AB như hình 9.11. Trên đoạn thẳng AB lấy điểm M sao cho AM = A'B'. Kẻ đường thẳng qua M song song với BC và cắt AC tại N.
- Hãy giải thích vì sao ΔAMN ∽ ΔABC
- Hãy chứng tỏ rằng AN=A’C’′, MN=B′C′ để suy ra ΔAMN = ΔA'B'C' (c.c.c)
- Hai tam giác A'B'C' và ABC có đồng dạng với nhau không? Nếu có, em hãy viết đúng kí hiệu đồng dạng giữa chúng.
c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC không? Vì sao?
Bài 25 :
Nếu ΔABC ∽ ΔA′B′C′ và anh Pi đo được A′C′=3,76cm thì khoảng cách từ bạn Tròn đến chân cột cờ là bao nhiêu mét?
Bài 26 :
Cho ΔABC ∽ ΔDEF. Biết \(\widehat A = {60^o};\widehat E = {80^o}\), hãy tính số đo các góc \(\widehat B,\widehat C,\widehat D,\widehat F\)
Bài 27 :
Cho ΔABC ∽ ΔA'B'C'. Biết AB=3cm, A′B′=6cm và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C'
Bài 28 :
Cho ABC là tam giác không cân. Biết ΔA′B′C′ ∽ ΔABC. Khẳng định nào sau đây là đúng?
A. ΔA′C′B′ ∽ ΔACB
B. ΔB′C′A′ ∽ ΔBAC
C. ΔB′A′C′ ∽ ΔBCA
D. ΔA′C′B′ ∽ ΔABC
Bài 29 :
Cho ΔA′B′C′ ∽ ΔABC với tỉ số đồng dạng bằng 2. Khẳng định nào sau đây là đúng:
A. \(\frac{{AB}}{{A'B'}} = 2\)
B. \(\frac{{AB}}{{A'C'}} = 2\)
C. \(\frac{{A'B'}}{{AB}} = 2\)
D. \(\frac{{A'B'}}{{AC}} = 2\)
Bài 30 :
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Điều nào dưới đây không suy ra ΔABC ∽ ΔDEF
A. \(\widehat B = \widehat E\)
B. \(\widehat C = \widehat F\)
C. \(\widehat B + \widehat C = \widehat E + \widehat F\)
D. \(\widehat B - \widehat C = \widehat E - \widehat F\)












