Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC vuông tại A, \(AB = a\sqrt 3 \), AC = AA’ = a. Giá trị sin của góc giữa đường thẳng AC’ và mặt phẳng (BCC’B’) bằng

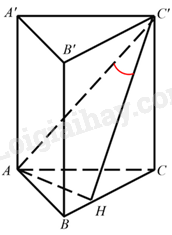
Xét \(\Delta ABC\) vuông tại \(A:\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Leftrightarrow AH = \frac{{\sqrt 3 }}{2}a\).

Xét \(\Delta AA'C'\) vuông tại C’: \(AC' = {\rm{ }}\sqrt {AA{'^2} + AC{'^2}} {\rm{ \;}} = a\sqrt 2 \).

Xét \(\Delta AHC'\) vuông tại C’: \(\sin \widehat {AC'H} = \frac{{AH}}{{A{C^\prime }}} = \frac{{\sqrt 6 }}{4}\).

Đáp án D.