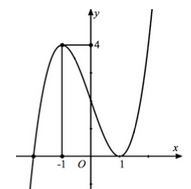
Cho hàm số $y = f\left( x \right)$ liên tục trên $R$ và có đồ thị như hình vẽ bên, một hàm số $g\left( x \right)$ xác định theo $f\left( x \right)$ có đạo hàm $g'\left( x \right) = f\left( x \right) + m$. Tìm tất cả các giá trị thực của tham số $m$ để hàm số $g\left( x \right)$ có duy nhất một cực trị.

Hàm số $g\left( x \right)$ có duy nhất một cực trị $\Leftrightarrow$ pt $g'\left( x \right) = 0$ có đúng một nghiệm $x_0$ thỏa mãn $g'(x)$ đổi dấu qua nghiệm đó.

Theo đề bài ta có: $g'\left( x \right) = f\left( x \right) + m$ $\Rightarrow g'\left( x \right) = 0 \Leftrightarrow f\left( x\right) + m = 0 \Leftrightarrow f\left( x \right) =  - m$ $\Rightarrow$ Số nghiệm của pt $g'\left( x \right) = 0$ là số giao điểm của đồ thị hàm số $y = f\left( x \right)$ và đường thẳng $y =  - m$.

Quan sát đồ thị ta thấy đường thẳng $y =  - m$ cắt đồ thị hàm số $y = f\left( x \right)$ tại một điểm duy nhất

$\Leftrightarrow \left[ \begin{gathered}  - m < 0 \hfill \\ - m > 4 \hfill \\ \end{gathered}  \right. \Leftrightarrow \left[ \begin{gathered}m > 0 \hfill \\  m <  - 4 \hfill \\ \end{gathered}  \right.$.

Ngoài ra, với $m=0$ hoặc $m=-4$ thì đồ thị hàm số $y=f(x)$ có hai điểm chung với đường thẳng $y=m$ nhưng một điểm là điểm tiếp xúc nên phương trình $g'(x)=0$ có hai nghiệm phân biệt, trong đó có một nghiệm kép và một nghiệm đơn.

Nên trong trường hợp này, hàm số $y=g(x)$ vẫn chỉ có một cực trị.

Vậy $m \ge 0$ hoặc $m \le  - 4$.