Cho trục số được vẽ trên lưới ô vuông đơn vị như Hình 1.

a) Tính độ dài cạnh huyền OB của tam giác vuông OAB.

b) Vẽ đường tròn tâm O bán kính OB, đường tròn này cắt trục số tại hai điểm P và Q.

Gọi x là số thực được biểu diễn bởi điểm P, y là số thực được biểu diễn bởi điểm Q.

Thay mỗi ? bằng số thích hợp để có các đẳng thức:

x² = ?, y² = ?.

Bài 1 :

Cho số thực $a > 0$. Số nào sau đây là căn bậc hai số học của $a$ ?

Bài 2 :

Số nào sau đây là căn bậc hai số học của số $a = 0,36.$

Bài 3 :

Cho số thực $a > 0$. Căn bậc hai số học của $a$ là $x$ khi và chỉ khi

Bài 4 :

Số nào sau đây là căn bậc hai số học của số $a = 2,25$

Bài 5 :

Tìm các số thực x sao cho ${x^2} = 49.$

Bài 6 :

Tìm căn bậc hai của 121.

Bài 7 :

Căn bậc hai của 4 là

A. 2.

B. -2.

C. 2 và -2.

D. $\sqrt 2$ và $- \sqrt 2 .$

Bài 8 :

Căn bậc hai số học của 49 là

A. 7.

B. -7.

C. 7 và -7.

D. $\sqrt 7$ và $- \sqrt 7 .$

Bài 9 :

Tính các căn bậc hai của mỗi số sau:

a) 36

b) $\frac{4}{{49}}$

c) 1,44

d) 0

Bài 10 :

Sử dụng dấu căn bậc hai để viết các căn bậc hai của mỗi số:

a) 11

b) 2,5

c) – 0,09

Bài 11 :

Tính

a) $\sqrt {1600}$

b) $\sqrt {0,81}$

c) $\sqrt {\frac{9}{{25}}}$

Bài 12 :

Tính giá trị của các biểu thức:

a) ${\left( {\sqrt {12} } \right)^2}$

b) ${\left( { - \sqrt {0,36} } \right)^2}$

c) ${\left( {\sqrt 5 } \right)^2} + {\left( { - \sqrt {1,21} } \right)^2}$

Bài 13 :

Biết rằng hình A và hình vuông B trong Hình 2 có diện tích bằng nhau. Tính độ dài cạnh x của hình vuông B.

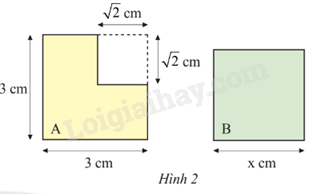
Bài 14 :

Tìm các căn bậc hai của mỗi số sau:

a) 16

b) 2500

c) $\frac{4}{{81}}$

d) 0,09

Bài 15 :

Tính

a) $\sqrt {100}$

b) $\sqrt {225}$

c) $\sqrt {2,25}$

d) $\sqrt {\frac{{16}}{{225}}}$

Bài 16 :

Biết rằng 25² = 625, tìm các căn bậc hai của các số 625 và 0,0625

Bài 17 :

Biết rằng ${\left( {2,6} \right)^2} = 6,76$, giá trị của biểu thức $\sqrt {0,0676}$ bằng

A. 0,0026

B. 0,026

C. 0,26

D. 2,6

Bài 18 :

Một trục số được vẽ trên lưới ô vuông như Hình 1.

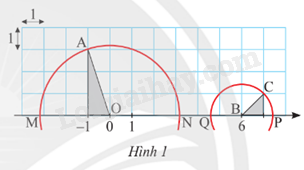
a) Đường tròn tâm O bán kính OA cắt trục số tại hai điểm M và N. Hai điểm M và N biểu diễn hai số thực nào?

b) Đường tròn tâm B bán kính BC cắt trục số tại hai điểm P và Q. Hai điểm P và Q biểu diễn hai số thực nào?

Bài 19 :

Một bàn cờ vua có dạng hình vuông gồm 64 ô vuông nhỏ (Hình 1). Hỏi mỗi cạnh của bàn cờ gồm bao nhiêu cạnh ô vuông nhỏ?

Bài 20 :

Tìm các số thực $x$ sao cho:

a. ${x^2} = 9$

b. ${x^2} = 25$

Bài 21 :

Tìm căn bậc hai của: $256;\,\,0,04;\,\,\frac{{121}}{{36}}$.

Bài 22 :

Tìm căn bậc hai của:

a. $289$

b. $0,81$

c. $1,69$

d. $\frac{{49}}{{121}}$

Bài 23 :

Đại Kim tự tháp Giza là Kim tự tháp Ai Cập lớn nhất và là lăng mộ của Vương triều thứ Tư của pharaoh Khufu. Nền kim tự tháp có dạng hình vuông với diện tích khoảng $53052{m^2}$. Hỏi độ dài cạnh nền của kim tự tháp đó là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Bài 24 :

Căn bậc hai của 16 là:

A. 4.

B. 4 và – 4.

C. 256.

D. 256 và – 256. 

Bài 25 :

Nếu $\sqrt x  = 9$ thì $x$ bằng:

A. 3.

B. 3 hoặc – 3.

C. 81.

D. 81 hoặc – 81.

Bài 26 :

a) Tìm căn bậc hai số học của 4.

b) Xét số đối của căn bậc hai số học của 4. Tính bình phương của số này và so sánh kết quả với 4.

Bài 27 :

Tìm các căn bậc hai của mỗi số sau:

a) 16;

b) $\frac{9}{{25}}$;

c) 0,36;

d) 6

Bài 28 :

So sánh:

a) 2 và $\sqrt 5$;

b) 7 và $\sqrt {48}$.

Bài 29 :

Bạn Tuấn khẳng định: “Có đúng một số thực sao cho bình phương tổng của số này với 1 là 36”. Bạn Mai khẳng định: “Có đúng hai số thực như thế”. Trong hai bạn Tuấn và Mai, ai đúng ai sai? Vì sao?

Bài 30 :

Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng:

a) 169;

b) 256;       

c) 324;       

d) 400.