Nội dung từ Loigiaihay.Com
Cho tam giác ABC vuông tại A có AC = 10 cm, \(\widehat C = {60^o}\). Độ dài hai cạnh còn lại là:
A. \(AB = \frac{{5\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm\)
B. \(AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{14\sqrt 3 }}{3}cm\)
C. \(AB = 10\sqrt 3 cm;BC = 20cm\)
D. \(AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm\)
Đọc kĩ dữ liệu đề bài để vẽ hình
Dựa vào định lí: Xét tam giác vuông :
+ Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.
+ Áp dụng định lý Pythagore trong tam giác vuông tìm cạnh góc vuông còn lại.
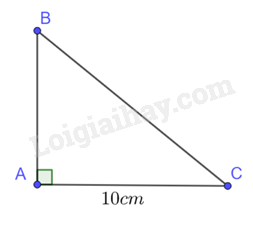
Xét tam giác ABC vuông tại A, \(\widehat C = {60^o}\), ta có:
AB = tan\(\widehat C\). AC = tan\({60^o}\). 10 = 10\(\sqrt 3 \) cm
BC = \(\frac{{AC}}{{\sin \widehat C}} = \frac{{10}}{{\sin {{60}^o}}} = \frac{{20\sqrt 3 }}{3}\)cm.
Không có đáp án đúng.

Các bài tập cùng chuyên đề
Bài 1 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Chọn khẳng định sai?
-
A.
\(b = a.\sin B = a.\cos C\)
-
B.
$a = c.\tan B = c.\cot C$
-
C.
${a^2} = {b^2} + {c^2}$
-
D.
\(c = a.\sin C = a.\cos B\)
Bài 2 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 10\,cm,\widehat C = 30^\circ .\) Tính $AB;BC$
-
A.
$AB = \dfrac{{5\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$
-
B.
$AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{14\sqrt 3 }}{3}$
-
C.
$AB = \dfrac{{10\sqrt 3 }}{3};BC = 20\sqrt 3 $
-
D.
$AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$
Bài 3 :
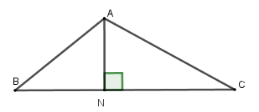
Cho tam giác $ABC$ có $BC = 11cm,\widehat {ABC} = 40^\circ $ và $\widehat {ACB} = {30^0}.$ Gọi $N$ là chân đường vuông góc hạ từ $A$ xuống cạnh $BC$.
Bài 4 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c,\widehat {ABC} = 50^\circ \) Chọn khẳng định đúng?
-
A.
\(b = c.\sin 50^\circ \)
-
B.
\(b = a.\tan 50^\circ \)
-
C.
\(b = c.\cot 50^\circ \)
-
D.
\(c = b.\cot 50^\circ \)
Bài 5 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 20\,cm,\widehat C = 60^\circ .\) Tính \(AB;BC\)
-
A.
\(AB = 20\sqrt 3 ;BC = 40\)
-
B.
\(AB = 20\sqrt 3 ;BC = 40\sqrt 3 \)
-
C.
\(AB = 20;BC = 40\)
-
D.
\(AB = 20;BC = 20\sqrt 3 \)
Bài 6 :
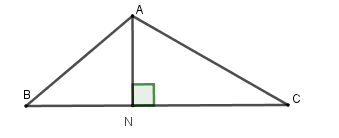
Cho tam giác \(ABC\) có \(BC = 9cm,\widehat {ABC} = 50^\circ \) và \(\widehat {ACB} = {35^0}.\) Gọi \(N\) là chân đường vuông góc hạ từ \(A\) xuống cạnh \(BC\).
Bài 7 :
Cho hình thang ABCD (AD // BC) có \(AD = 16cm,BC = 4cm,\widehat A = \widehat B = \widehat {ACD} = {90^0}.\)
a) Kẻ đường cao CE của tam giác ACD. Chứng minh \(\widehat {ADC} = \widehat {ACE}.\) Tính sin của các góc \(\widehat {ADC},\widehat {ACE}\) và suy ra \(A{C^2} = AE.AD.\) Từ đó tính AC.
b) Tính góc D của hình thang.
Bài 8 :
Một cuốn sách khổ \(17 \times 24\) cm, tức là chiều rộng 17 cm, chiều dài 24 cm. Gọi \(\alpha \) là góc giữa đường chéo và cạnh 17 cm. Tính \(\sin \alpha ,\cos \alpha \) (làm tròn đến chữ số thập phân thứ hai) và tính số đo \(\alpha \) (làm tròn đến độ) .
Bài 9 :
Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết \(HB = 3cm,HC = 6cm,\widehat {HAC} = {60^0}.\) Hãy tính độ dài các cạnh (làm tròn đến cm) , số đo các góc của tam giác ABC (làm tròn đến độ) .
Bài 10 :
Tính các số liệu còn thiếu (dấu “?”) ở Hình 4.28 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.
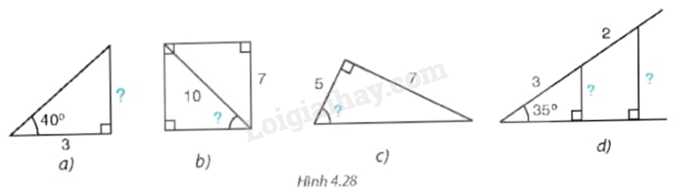
Bài 11 :
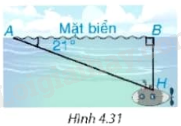
Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển theo đường thẳng tạo với mặt nước một góc \({21^0}\) để lặn xuống (H.4.31) .
a) Khi tàu chuyển động theo hướng đó và đi được 200 m thì tàu ở độ sâu bao nhiêu so với mặt nước biển? (làm tròn đến m) .
b) Giả sử tốc độ của tàu là 9 km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sau 200 m (tức là cách mặt nước biển 200 m) ?
Bài 12 :
Để đo khoảng cách giữa hai điểm A và B không tới được, một người đứng ở điểm H sao cho B ở giữa A và H rồi dịch chuyển đến điểm K sao cho KH vuông góc với AB tại H, \(HK = a\left( m \right)\), ngắm nhìn A với \(\widehat {AKH} = \alpha \), ngắm nhìn B với \(\widehat {BKH} = \beta \left( {\alpha > \beta } \right)\).
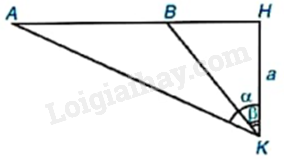
a) Hãy biểu diễn AB theo \(a,\alpha ,\beta \).
b) Khi \(a = 3m,\alpha = {60^o},\beta = {30^o}\), hãy tính AB (làm tròn kết quả đến chữ số thập phân thứ ba của mét).
Bài 13 :
Cho tam giác ABC vuông tại B có góc \(\widehat A = {30^o},AB = 6cm\). Vẽ tia Bt sao cho \(\widehat {tBC} = {30^o}\), cắt tia AC ở D (C nằm giữa A và D).
a) Chứng minh tam giác ABD cân tại B.
b) Tính khoảng cách từ D đến đường thẳng AB.
Bài 14 :
Cho tam giác ABC vuông tại A (Hình 1).
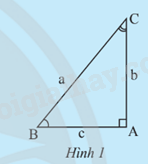
a) Hãy tính sin B theo b và a, cos B theo c và a. Sử dụng các kết quả tính được để giải thích tại sao ta lại có các đẳng thức:
b = a.sin B
c = a.cos B
b) Hãy tính tan B theo b và c, cot B theo c và b. Sử dụng các kết quả tính được ở trên để giải thích tại sao ta lại có các đẳng thức:
b = c.tan B
c = b.cot B.
Bài 16 :
Cho tam giác \(ABC\) có đường cao \(AH = 6cm,\widehat B = 40^\circ ,\widehat C = 35^\circ \). Tính độ dài các đoạn thẳng \(AB,BH,AC,BC\) (làm tròn kết quả đến hàng phần mười của centimét).
Bài 17 :
Trong Hình 24, cho \(\widehat O = \alpha ,AB = m\) và \(\widehat {OAB} = \widehat {OCA} = \widehat {ODC} = 90^\circ \).
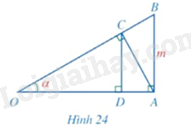
Chứng minh:
a) \(OA = m.\cot \alpha \);
b) \(AC = m.\cos \alpha \);
c) \(CD = m.{\cos ^2}\alpha \).
Bài 18 :
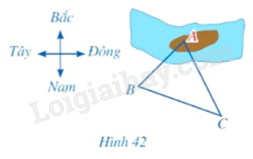
Một người đứng ở vị trí \(B\) trên bờ sông muốn sử dụng la bàn để ước lượng khoảng cách từ vị trí đó đến một vị trí \(A\) ở trên một cù lao giữa dòng sông. Người đó đã làm như sau:
- Sử dụng la bàn, xác định được phương \(BA\) lệch với phương Nam – Bắc về hướng Đông \(52^\circ \).
- Người đó di chuyển đến vị trí \(C\), cách \(B\) một khoảng là 187m. Sử dụng la bàn, xác định được phương \(CA\) lệch với phương Nam – Bắc về hướng Tây \(27^\circ \); \(CB\) lệch với phương Nam – Bắc về hướng Tây \(70^\circ \) (Hình 42).
Em hãy giúp người đó tính khoảng cách \(AB\) từ những dữ liệu trên (làm tròn kết quả đến hàng đơn vị của mét).
Bài 19 :
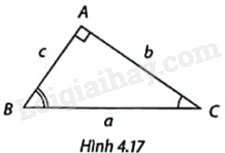
Cho \(\Delta ABC\) vuông tại A như Hình 4.17. Xác định tên các góc nhọn ở các ô ?:
Vì \(\frac{b}{a} = \cos ?\) nên \(b = a.\cos ?\);
Vì \(\frac{b}{a} = \sin ?\) nên \(b = a.\sin ?\);
Vì \(\frac{b}{c} = \tan ?\) nên \(b = c.\tan ?\);
Vì \(\frac{b}{c} = \cot ?\) nên \(b = c.\cot ?\);
Bài 20 :
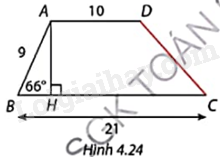
Tính độ dài cạnh bên CD của hình thang ABCD trong Hình 4.24.
Bài 21 :
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.
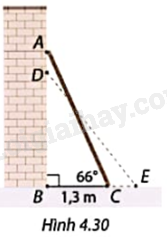
Một chiếc thang AC được dựng vào một bức tường thẳng đứng (Hình 4.30).
a) Ban đầu, khoảng cách từ chân thang đến tường là \(BC = 1,3m\) và góc tạo bởi thang và phương nằm ngang là \(\widehat {ACB} = {66^o}\), tính độ dài của thang.
b) Nếu đầu A của thang bị trượt xuống 40cm đến vị trí D thì góc DEB tạo bởi thang và phương nằm ngang khi đó bằng bao nhiêu?
Bài 22 :
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.
Trong Hình 4.32, mặt tiền mái nhà có chiều rộng \(BC = 3m\) và hai bên mái AB, AC cùng bằng 1,8m.
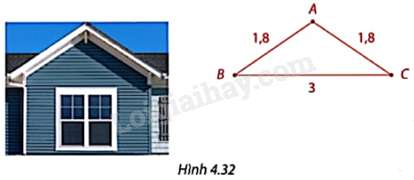
a) Tính chiều cao AH của mái nhà.
b) Tính góc BAC tạo bởi hai mép của mái nhà.
Bài 23 :
Trong Hình 4.35, tỉ số \(\frac{{BC}}{{AH}}\) bằng
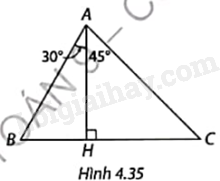
A. \(\frac{{\sqrt 3 }}{3} + 1\).
B. \(\sqrt 3 + 1\).
C. \(\frac{{\sqrt 2 }}{2} + 1\).
D. \(\sqrt 2 + 1\).
Bài 24 :
Cho hình vẽ
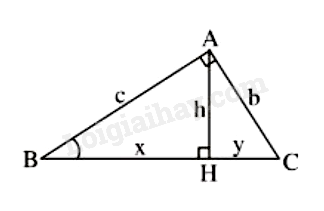
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) \(h = b.\sin B\)
b) \(BC = \frac{c}{{\sin C}}\)
c) \({b^2} = x.y\)
d) \({\sin ^2}B + {\cos ^2}C = 1\)
e) \(\cos C = \frac{h}{b}\)
Bài 25 :
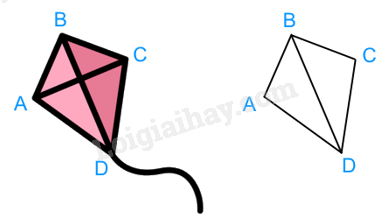
Một chiếc diều ABCD có \(AB = BC,AD = DC\). Biết \(AB = 12cm,\widehat {ADC} = 40^\circ ,\widehat {ABC} = 90^\circ \). Chiều dài cạnh AD và diện tích của chiếc diều là: (làm tròn đến hàng phần trăm)
-
A.
\(AD \approx 24,8cm,{S_{ABCD}} \approx 269,9\).
-
B.
\(AD \approx 24,8cm,{S_{ABCD}} \approx 269,8\).
-
C.
\(AD \approx 24,8cm,{S_{ABCD}} \approx 269,7\).
-
D.
\(AD \approx 24,9cm,{S_{ABCD}} \approx 269,8\).
Bài 26 :
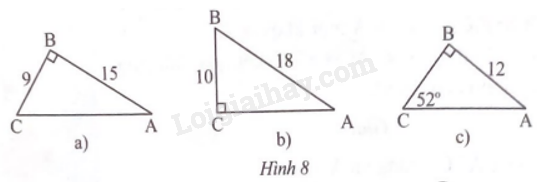
Giải tam giác vuông ABC trong mỗi trường hợp sau:
Bài 27 :
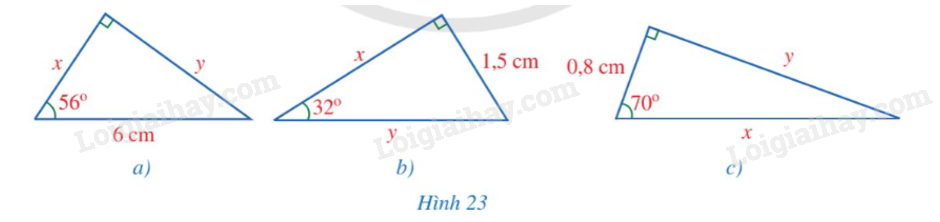
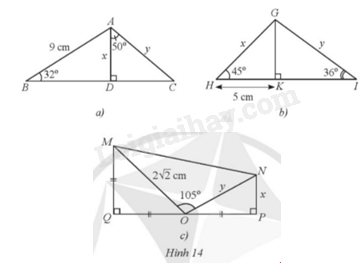
Tìm x, y trong mỗi hình 14a, 14b, 14c (làm tròn kết quả đến hàng phần mười của centimet).
Bài 28 :
Cho tam giác ABC vuông tại A. Chứng minh \(\tan \frac{{\widehat B}}{2} = \frac{{AC}}{{AB + BC}}\)
Bài 29 :
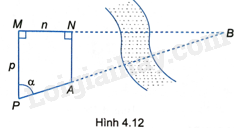
Cho A, B là hai địa điểm ở hai bên bờ sông, biết AN và PM cùng vuông góc MN, \(MN = n\) (mét), \(MP = p\) (mét), \(p > n\) và \(\widehat {MPA} = \alpha \) (H.4.12). Chứng minh rằng: \(AB = \frac{{p\tan \alpha - n}}{{\sin \alpha }}\).
Bài 30 :
Chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Tam giác ABC vuông tại A, có AB = 24 cm, BC = 25 cm, AH là đường cao (Hình 5).
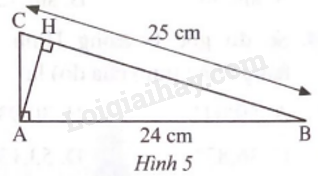
a) AC = 8 cm
b) \(\widehat B \approx {16,26^o}\)
c) \({\rm{cosC = }}\frac{{24}}{{25}}\)
D. \(AH \approx 7\)