Nội dung từ Loigiaihay.Com
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\). Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm thời điểm vật đạt độ cao lớn nhất:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Xét hàm số: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\).
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \[h'\left( t \right) = - 9,8t + 24,5;h'\left( t \right) = 0 \Leftrightarrow - 9,8t + 24,5 = 0 \Leftrightarrow t = \frac{5}{2}\].
Bảng biến thiên:
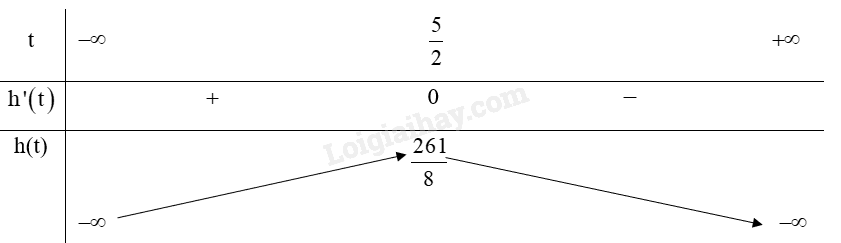
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(t = \frac{5}{2}\),
Vậy thời điểm vật đạt độ cao lớn nhất là \(t = \frac{5}{2}\) giây

Các bài tập cùng chuyên đề
Bài 1 :
Hàm số nào dưới đây có giá trị nhỏ nhất trên tập xác định?
-
A.
\(y = {x^3} - 3x + 2\)
-
B.
\(y = - 2{x^3} + 3{x^2} - 1\)
-
C.
\(y = {x^4} - 2{x^2} - 1\)
-
D.
\(y = - {x^4} + 4{x^2}\)
Bài 2 :
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = \sqrt {2x - {x^2}} \);
b) \(y = - x + \frac{1}{{x - 1}}\) trên khoảng \(\left( {1; + \infty } \right)\).
Bài 3 :
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) \(y = 2{x^3} - 3{x^2} + 5x + 2\) trên đoạn \(\left[ {0;2} \right]\);
b) \(y = \left( {x + 1} \right){e^{ - x}}\) trên đoạn \(\left[ { - 1;1} \right]\).
Bài 4 :
Xét hàm số \(y = f\left( x \right) = {x^3} - 2{x^2} + 1\) trên đoạn \(\left[ { - 1;2} \right]\), với đồ thị như Hình 1.16.

a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 1;2} \right]\).
b) Tính đạo hàm f’(x) và tìm các điểm \(x \in \left( { - 1;2} \right)\) mà \(f'\left( x \right) = 0\).
c) Tính giá trị của hàm số tại hai đầu mút của đoạn \(\left[ { - 1;2} \right]\) và tại các điểm x đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với \(\mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right)\), số lớn nhất trong các giá trị này với \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} f\left( x \right)\).
Bài 5 :
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = - {x^2} + 4x + 3\);
b) \(y = {x^3} - 2{x^2} + 1\) trên \(\left[ {0; + \infty } \right)\);
c) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) trên \(\left( {1; + \infty } \right)\);
d) \(y = \sqrt {4x - 2{x^2}} \).
Bài 6 :
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = {x^4} - 2{x^2} + 3\);
b) \(y = x.{e^{ - x}}\);
c) \(y = x\ln x\);
d) \(y = \sqrt {x - 1} + \sqrt {3 - x} \).
Bài 7 :
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = 2{x^3} - 6x + 3\) trên đoạn \(\left[ { - 1;2} \right]\);
b) \(y = {x^4} - 3{x^2} + 2\) trên đoạn \(\left[ {0;3} \right]\);
c) \(y = x - \sin 2x\) trên đoạn \(\left[ {0;\pi } \right]\);
d) \(y = \left( {{x^2} - x} \right){e^x}\) trên đoạn \(\left[ {0;1} \right]\).
Bài 8 :
Giá trị lớn nhất của hàm số \(y = {\left( {x - 2} \right)^2}.{e^x}\) trên đoạn [1; 3] là:
A. 0.
B. \({e^3}\).
C. \({e^4}\).
D. e.
Bài 9 :
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = \frac{{2x + 1}}{{3x - 2}}\) trên nửa khoảng \(\left[ {2; + \infty } \right)\);
b) \(y = \sqrt {2 - {x^2}} \);
Bài 10 :
Giá trị lớn nhất M của hàm số \(y = \frac{{{x^2} + 3}}{{x - 1}}\) trên đoạn [2; 4] là
A. \(M = 6\).
B. \(M = 7\).
C. \(M = \frac{{19}}{3}\).
D. \(M = \frac{{20}}{3}\).
Bài 11 :
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) \(y = \frac{{x + 1}}{{\sqrt {{x^2} + 1} }}\) trên đoạn \(\left[ { - 1;2} \right]\);
b) \(y = x + \sqrt {1 - {x^2}} \)
Bài 12 :
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(f\left( x \right) = \sqrt {9 - {x^2}} \) trên đoạn \(\left[ { - 3;3} \right]\).
Bài 13 :
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \sin 2x - 2x\) trên đoạn \(\left[ {\frac{\pi }{2};\frac{{3\pi }}{2}} \right]\).
Bài 14 :
Cho hàm số \(y = f\left( x \right) = 2{x^3} - 6x,x \in \left[ { - 2;2} \right]\) có đồ thị là đường cong ở Hình 9.
a) Dựa vào đồ thị ở Hình 9, hãy cho biết các giá trị \(M = \mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right);m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right)\) bằng bao nhiêu.
b) Giải phương trình \(f'\left( x \right) = 0\) với \(x \in \left( { - 2;2} \right)\)
c) Tính các giá trị của hàm số \(f\left( x \right)\) tại hai đầu mút \( - 2;2\) và tại các điểm \(x \in \left( { - 2;2} \right)\) mà ở đó \(f'\left( x \right) = 0\)
d) So sánh M (hoặc m) với số lớn nhất (hoặc số bé nhất) trong các giá trị tính được ở câu c

Bài 15 :
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số \(y = \frac{{2x - 5}}{{x - 1}}\) trên nửa khoảng \((1;3]\).
Bài 16 :
Cho hàm số \(f\left( x \right) = x + \frac{1}{{x - 1}}\) với \(x > 1\).
a) Tính \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\).
b) Lập bảng biến thiên của hàm số \(f\left( x \right)\) trên khoảng \(\left( {1; + \infty } \right)\).
c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số \(f\left( x \right)\) trên khoảng \(\left( {1; + \infty } \right)\).
Bài 17 :
Tìm giá trị lớn nhất của mỗi hàm số sau:
a) \(f\left( x \right) = \frac{4}{{1 + {x^2}}}\).
b) \(f\left( x \right) = x - \frac{3}{x}\) trên nửa khoảng \((0;3]\).
Bài 18 :
Tìm giá trị nhỏ nhất của mỗi hàm số sau:
a) \(f\left( x \right) = x + \frac{4}{x}\) trên khoảng \(\left( {0; + \infty } \right)\)
b) \(f\left( x \right) = {x^3} - 12x + 1\) trên khoảng \(\left( {1; + \infty } \right)\)
Bài 19 :
Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau:
a) \(f\left( x \right) = {x^3} - \frac{3}{2}{x^2}\) trên đoạn \(\left[ { - 1;2} \right]\)
b) \(f\left( x \right) = {x^4} - 2{x^3} + {x^2} + 1\) trên đoạn \(\left[ { - 1;1} \right]\)
c) \(f\left( x \right) = {e^x}\left( {{x^2} - 5x + 7} \right)\) trên đoạn \(\left[ {0;3} \right]\)
d) \(f\left( x \right) = \cos 2x + 2x + 1\) trên đoạn \(\left[ {\frac{{ - \pi }}{2};\pi } \right]\)
Bài 20 :
Tìm giá trị nhỏ nhất và giá trị lớn nhất của mỗi hàm số sau:
a) \(f\left( x \right) = 2{x^3} - 6x\) trên đoạn \(\left[ { - 1;3} \right]\);
b) \(f\left( x \right) = \frac{{{x^2} + 3x + 6}}{{x + 2}}\) trên đoạn \(\left[ {1;5} \right]\);
c) \(f\left( x \right) = \frac{{In\left( {x + 1} \right)}}{{x + 1}}\) trên đoạn \(\left[ {0;3} \right]\);
d) \(f\left( x \right) = 2sin3x + 7x + 1\) trên đoạn \(\left[ {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right]\)
Bài 21 :
Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu?
Bài 22 :
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(g(x) = x + \frac{4}{{{x^2}}}\) trên đoạn [1;4]
Bài 23 :
Hình 3 cho ta đồ thị của ba hàm số
\(f(x) = \frac{1}{2}{x^2}\); \(g(x) = \left\{ \begin{array}{l}\frac{1}{2}{x^2}\;\;\;\;\;\;\;\;\;\;\;neu\;x \le 2\;\\ - 4x + 10\;\;\;\;neu\;x \ge 2\end{array} \right.\) và \(h(x) = 3 - \frac{1}{2}{x^2}\) trên đoạn [-1;3]
a) Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó?
b) Các hàm số còn lại đạt giá trị lớn nhất tại điểm nào?

Bài 24 :
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x^3} - 12x + 1\) trên đoạn [-1;3]
b) \(y = - {x^3} + 24{x^2} - 180x + 400\) trên đoạn [3;11]
c) \(y = \frac{{2x + 1}}{{x - 2}}\) trên đoạn [3;7]
d) \(y = \sin 2x\) trên đoạn \([0;\frac{{7\pi }}{{12}}]\)
Bài 25 :
Tìm giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x^3} - 3x - 4\) trên nửa khoảng [-3;2).
b) \(y = \frac{{3{x^2} - 4x}}{{{x^2} - 1}}\) trên khoảng \(( 1; + \infty )\).
Bài 26 :
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 2\sqrt {1 - {x^2}} + {x^2}\)
Bài 27 :
Giá trị nhỏ nhất của hàm số \(y = \sqrt {{x^2} + 2x + 3} \) trên đoạn [–2; 3] là
A. \(\sqrt 3 \) B. \(\sqrt {30} \) C. \(\sqrt 2 \) D. 0
Bài 28 :
Giá trị lớn nhất của hàm số \({(x - 2)^2}.{e^x}\) trên đoạn \([0;3]\) bằng:
-
A.
0
-
B.
4
-
C.
\(e\)
-
D.
\({e^3}\)
Bài 29 :
Giá trị lớn nhất của hàm số \(\frac{{2x + 1}}{{x - 2}}\) trên đoạn \([ - \frac{1}{2};1]\) bằng:
-
A.
0
-
B.
\(\frac{1}{2}\)
-
C.
-3
-
D.
1
Bài 30 :
Giá trị lớn nhất của hàm số \(y = x{(5 - 2x)^2}\) trên [0;3] là một phân số có dạng \(\frac{a}{b}\). Tính a + 2b.












