Nội dung từ Loigiaihay.Com
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = - {x^3} + 3x + 1\);
b) \(y = {x^3} + 3{x^2} - x - 1\).
Phương pháp giải
Sử dụng kiến thức về sơ đồ khảo sát hàm số bậc ba để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số bậc ba
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải của GV HocTot.XYZ
a) Tập xác định: \(D = \mathbb{R}\)
2. Sự biến thiên:
Ta có: \(y' = - 3{x^2} + 3,y' = 0 \Leftrightarrow x = \pm 1\)
Trên khoảng \(\left( { - 1;1} \right)\), \(y' > 0\) nên hàm số đồng biến. Trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\), \(y' < 0\) nên hàm số nghịch biến trên mỗi khoảng đó.
Hàm số đạt cực đại tại \(x = 1\), giá trị cực đại \({y_{CĐ}}=3\) . Hàm số đạt cực tiểu tại \(x = - 1\), giá trị cực tiểu \({y_{CT}} = - 1\)
Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 3x + 1} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^3}\left( { - 1 + \frac{3}{{{x^2}}} + \frac{1}{{{x^3}}}} \right)} \right] = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - {x^3} + 3x + 1} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {{x^3}\left( { - 1 + \frac{3}{{{x^2}}} + \frac{1}{{{x^3}}}} \right)} \right] = - \infty \)
Bảng biến thiên:
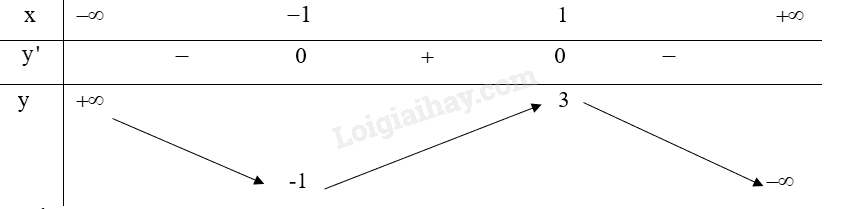
3. Đồ thị:
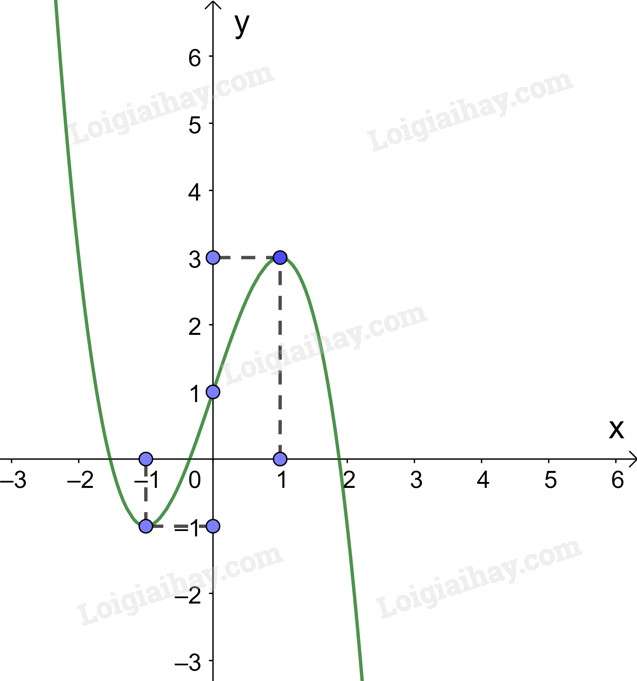
Giao điểm của đồ thị hàm số \(y = - {x^3} + 3x + 1\) với trục tung là (0; 1).
Các điểm (1; 3); \(\left( { - 1; - 1} \right)\) thuộc đồ thị hàm số \(y = - {x^3} + 3x + 1\).
Đồ thị hàm số có tâm đối xứng là điểm (0; 1).
b) 1. Tập xác định: \(D = \mathbb{R}\)
2. Sự biến thiên:
Ta có: \(y' = 3{x^2} + 6x - 1,y' = 0 \Leftrightarrow x = \frac{{ - 3 - 2\sqrt 3 }}{3}\) hoặc \(x = \frac{{ - 3 + 2\sqrt 3 }}{3}\)
Trên khoảng \(\left( {\frac{{ - 3 - 2\sqrt 3 }}{3};\frac{{ - 3 + 2\sqrt 3 }}{3}} \right)\), \(y' < 0\) nên hàm số nghịch biến. Trên khoảng \(\left( { - \infty ;\frac{{ - 3 - 2\sqrt 3 }}{3}} \right)\) và \(\left( {\frac{{ - 3 + 2\sqrt 3 }}{3}; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến trên mỗi khoảng đó.
Hàm số đạt cực đại tại \(x = \frac{{ - 3 - 2\sqrt 3 }}{3}\), giá trị cực đại . Hàm số đạt cực tiểu tại \(x = \frac{{ - 3 + 2\sqrt 3 }}{3}\), giá trị cực tiểu \({y_{CT}} = \frac{{18 - 16\sqrt 3 }}{9}\).
Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} + 3{x^2} - x - 1} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^3}\left( {1 + \frac{3}{x} - \frac{1}{{{x^2}}} - \frac{1}{{{x^3}}}} \right)} \right] = - \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} + 3{x^2} - x - 1} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {{x^3}\left( {1 + \frac{3}{x} - \frac{1}{{{x^2}}} - \frac{1}{{{x^3}}}} \right)} \right] = + \infty \)
Bảng biến thiên:
3. Đồ thị:
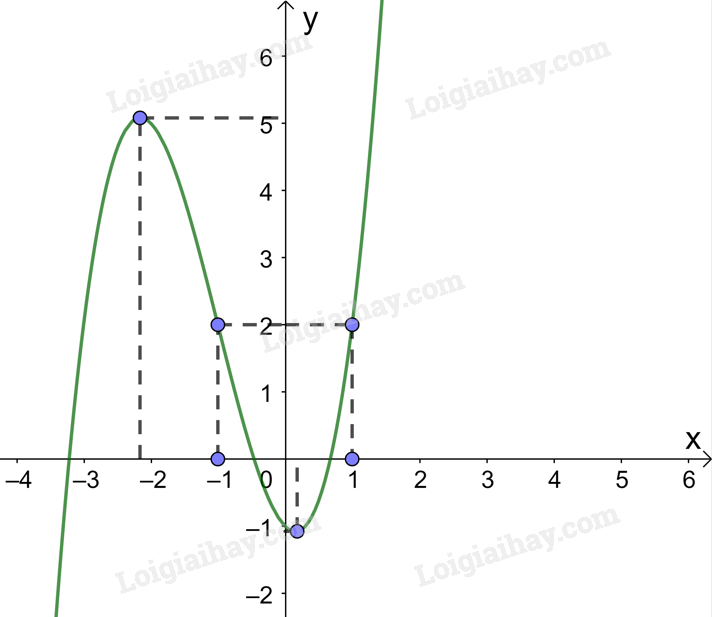
Giao điểm của đồ thị hàm số \(y = {x^3} + 3{x^2} - x - 1\) với trục tung là (0; -1).
Các điểm (-1; 2); \(\left( {1;2} \right)\) thuộc đồ thị hàm số \(y = {x^3} + 3{x^2} - x - 1\).
Đồ thị hàm số có tâm đối xứng là điểm (-1; 2).
Xem thêm : SGK Toán 12 - Kết nối tri thức
Các bài tập cùng chuyên đề
Bài 1 :
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - 2{x^3} + 3{x^2} - 5x\).
Xem lời giải >>
Bài 2 :
Đồ thị hàm số \(y = {x^3} - 3x - 1\) là đường cong sau ?
Xem lời giải >>
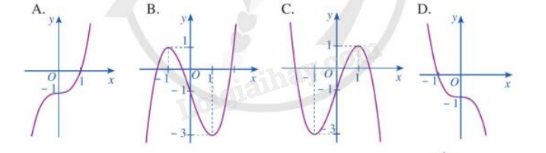
Bài 3 :
Đường cong ở hình 29 là đồ thị của hàm số:
Xem lời giải >>
Bài 4 :
khảo sát về sự biến thiên và vẽ đồ thị của các hàm số sau:
a,\(y = 2{x^3} - 3x + 1\)
b,\(y = - {x^3} + 3x - 1\)
c, \( y = {\left( {x - 2} \right)^3} + 4\)
d,\(y = - {x^3} + 3{x^2} - 1\)
e, \(y = \frac{1}{3}{x^3} + {x^2} + 2x + 1\)
g,\( y = - {x^3} - 3x\)
Xem lời giải >>
Bài 5 :
Hàm số nào có đồ thị như hình 32?
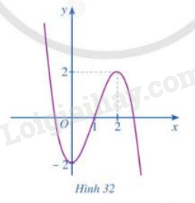
\(a,\;y = - {x^3} + 3x - 2\)
\(b,y = - {x^3} - 2\)
\(c,y = - {x^3} + 3{x^2} - 2\)
\(d,\;y = {x^3} - 3x - 2\)
Xem lời giải >>
Bài 6 :
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = - 2{x^3} - 3{x^2} + 1\)
b) \(y = {x^3} + 3{x^2} + 3x + 1\)
Xem lời giải >>
Bài 7 :
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = {x^3} + x - 2\)
b) \(y = 2{x^3} + {x^2} - \frac{1}{2}x - 3\)
Xem lời giải >>
Bài 8 :
Cho hàm số \(y = {x^3} - 3{x^2} + 2\)
a) Tìm điểm I thuộc đồ thị hàm số biết hoành độ của I là nghiệm của phương trình y’’ = 0.
b) Chứng minh rằng I là trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số.
Xem lời giải >>
Bài 9 :
Cho hàm số bậc ba y = f(x) có đồ thị như Hình 3. Viết công thức của hàm số
Xem lời giải >>
Bài 10 :
Cho hàm số \(y = \frac{1}{3}{x^3} - {x^2} + 4\).
a) Khảo sát và vẽ đồ thị của hàm số.
b) Tính khoảng cách giữa hai điểm cực trị của đồ thị hàm số.
Xem lời giải >>
Bài 11 :
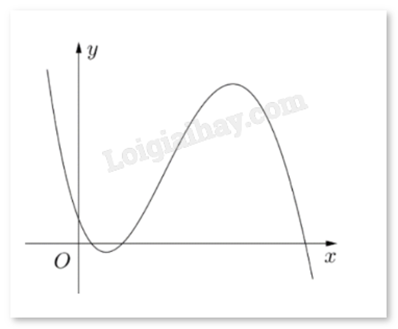
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) \((a,b,c,d \in \mathbb{R})\) có đồ thị là đường cong như hình bên. Có bao nhiêu số dương trong các số \(a,b,c,d\)?
Xem lời giải >>
Bài 12 :
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình vẽ sau:
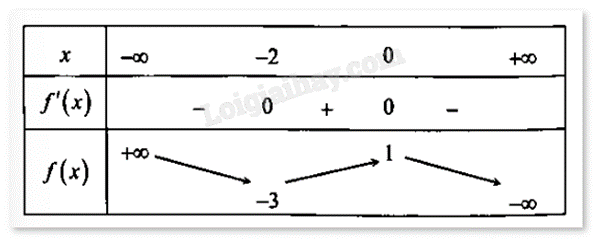
Xác định công thức của hàm số.
-
A.
\(y = {x^3} - 3{x^2} + 1\)
-
B.
\(y = - {x^3} - 2{x^2} + 1\)
-
C.
\(y = - {x^3} - 3{x^2} + 1\)
-
D.
\(y = - {x^3} + 3{x^2} + 1\)
Xem lời giải >>
Bài 13 :
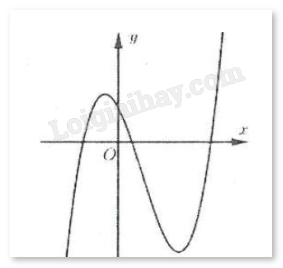
Đường cong hình bên là đồ thị của hàm số \(y = a{x^3} + b{x^2} + cx + d\). Khẳng định nào sau đây đúng?
-
A.
a > 0, b < 0, c > 0, d > 0
-
B.
a > 0, b < 0, c < 0, d > 0
-
C.
a > 0, b > 0, c < 0, d > 0
-
D.
a < 0, b > 0, c > 0, d < 0
Xem lời giải >>
Bài 14 :
Đường cong hình bên là đồ thị của hàm số \(y = a{x^3} + b{x^2} + cx + d\). Khẳng định nào sau đây đúng?
-
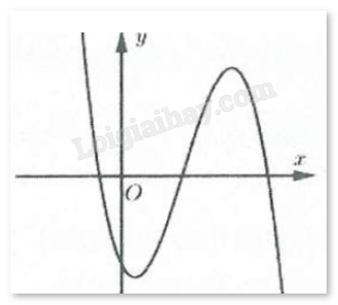
A.
a < 0, b < 0, c > 0, d < 0
-
B.
a > 0, b > 0, c < 0, d < 0
-
C.
a < 0, b < 0, c < 0, d > 0
-
D.
a < 0, b > 0, c < 0, d < 0
Xem lời giải >>
Bài 15 :
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = {x^3} - 6{x^2} + 9x\);
b) \(y = {x^3} + 3{x^2} + 6x + 4\).
Xem lời giải >>
Bài 16 :
Đồ thị hàm số \(y = 4{x^3} - 6x + 1\) là đường cong nào trong các đường cong sau?
Xem lời giải >>
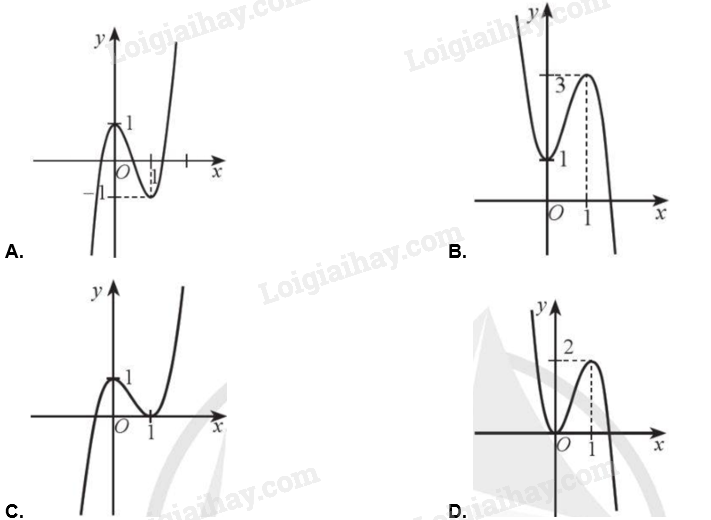
Bài 17 :
Đồ thị hàm số \(y = - {x^3} - x + 2\) là đường cong nào trong các đường cong sau?
Xem lời giải >>
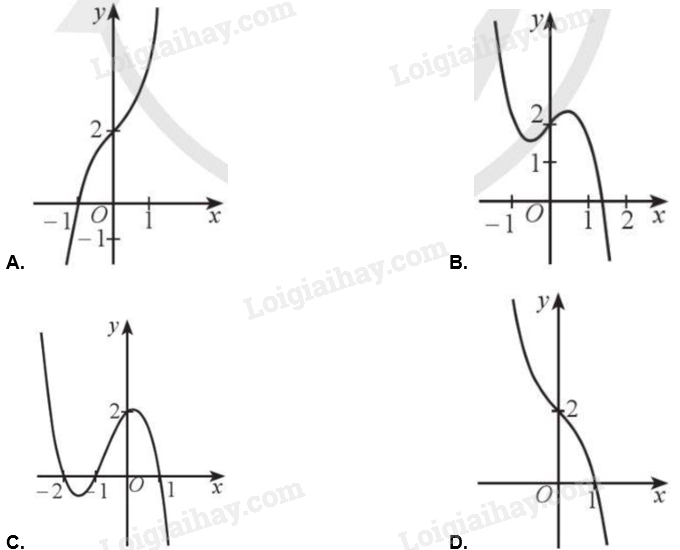
Bài 18 :
Đường cong ở Hình 16 là đồ thị của hàm số:
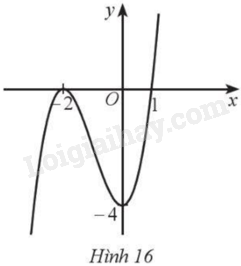
A. \(y = - \frac{{{x^3}}}{3} + {x^2} - 4\).
B. \(y = {x^3} - 3{{\rm{x}}^2} - 4\).
C. \(y = {x^3} + 3{{\rm{x}}^2} - 4\).
D. \(y = - {x^3} - 3{{\rm{x}}^2} + 4\).
Xem lời giải >>
Bài 19 :
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\) có đồ thị là đường cong ở Hình 20.
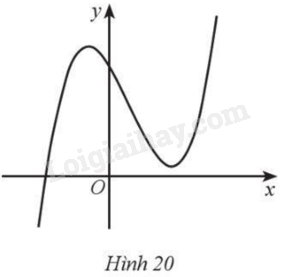
a) \(a > 0\).
b) Đồ thị cắt trục tung tại điểm có tung độ dương.
c) Đồ thị hàm số có hai điểm cực trị nằm cùng phía với trục tung.
d) \(b < 0\).
Xem lời giải >>
Bài 20 :
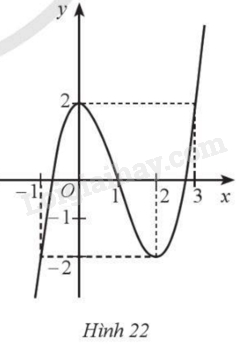
Cho hàm số bậc ba \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong như Hình 22. Căn cứ vào đồ thị hàm số:
a) Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số.
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 1;2} \right]\)
c) Tìm điểm trên đồ thị hàm số có hoành độ bằng 2.
d) Tìm điểm trên đồ thị hàm số có tung độ bằng 2.
e) Đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại mấy điểm?
g) Với giá trị nào của \(x\) thì \( - 2 < f\left( x \right) < 2\)?
h) Tìm công thức xác định hàm số \(f\left( x \right)\).
Xem lời giải >>
Bài 21 :
Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
a) \(y = \left( {x - 2} \right){\left( {x + 1} \right)^2}\);
b) \(y = - \frac{1}{3}{x^3} - {x^2} + 2\);
c) \(y = 2{{\rm{x}}^3} - 3{{\rm{x}}^2} + 2{\rm{x}} - 1\);
d) \(y = - \frac{1}{4}\left( {{x^3} - 6{{\rm{x}}^2} + 12{\rm{x}}} \right)\).
Xem lời giải >>
Bài 22 :
Đường cong ở Hình 27 là đồ thị của hàm số:
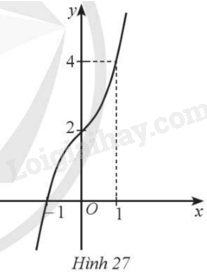
A. \(y = 2{{\rm{x}}^3} + 2\).
B. \(y = {x^3} - {x^2} + 2\).
C. \(y = - {x^3} + 3{\rm{x}} + 2\).
D. \(y = {x^3} + x + 2\).
Xem lời giải >>
Bài 23 :
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = x\left( {{x^2} - 4x} \right)\);
b) \(y = - {x^3} + 3{x^2} - 2\).
Xem lời giải >>
Bài 24 :
Cho hàm số \(y = \left( {m - 1} \right){x^3} + 2\left( {m + 1} \right){x^2} - x + m - 1\) (\(m\) là tham số).
a) Khảo sát và vẽ đồ thị của hàm số khi \(m = - 1\).
b) Tìm giá trị của \(m\) để tâm đối xứng của đồ thị hàm số có hoành độ \({x_0} = - 2\).
Xem lời giải >>
Bài 25 :
Cho hàm số \(y = 2{x^3} + 6{x^2} - x + 2\). Viết phương trình tiếp tuyến của đồ thị hàm số tại tâm đối xứng của nó.
Xem lời giải >>
Bài 26 :
Với giá trị nào của \(m\) thì đồ thị của hàm số \(y = - {x^3} - 3{x^2} + mx + 1\) có tâm đối xứng nằm trên trục \(Ox\)? Khi đó, có thể kết luận gì về số giao điểm của đồ thị hàm số với trục hoành?
Xem lời giải >>
Bài 27 :
Cho hàm số \(y = {x^3} - 3{x^2} + 2\) có đồ thị (C).
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến \(\Delta \) của đồ thị (C) tại tâm đối xứng của nó. Chứng minh rằng \(\Delta \) là tiếp tuyến có hệ số góc nhỏ nhất của (C).
c) Tìm các giá trị của tham số \(m\) để phương trình \({x^3} - 3{x^2} - m = 0\) có ba nghiệm phân biệt.
Xem lời giải >>
Bài 28 :
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = f(x) = - {x^3} + 2{x^2} + 4x - 3\)
b) \(y = f(x) = \frac{1}{3}{x^3} - {x^2} + x + 1\)
Xem lời giải >>
Bài 29 :
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = {x^3} + 3{x^2} - 4\)
b) \(y = {x^3} + 4{x^2} + 4x\)
c) \(y = - 2{x^3} + 2\)
d) \(y = - {x^3} - {x^2} - x + 1\)
Xem lời giải >>
Bài 30 :
Cho hàm số \(y = - {x^3} + 3x + 1\). Khảo sát sự biến thiên, vẽ đồ thị và chỉ ra tâm đối xứng của đồ thị hàm số đã cho.
Xem lời giải >>