Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a)      ${x^2} + 4x + 4$

b)      $16{a^2} - 16ab + 4{b^2}$

Bài 1 :

Thay  bằng biểu thức thích hợp.

a)      $\left( {x - 3y} \right)\left( {x + 3y} \right) = {x^2} - ?$;

b)      $\left( {2x - y} \right)\left( {2x + y} \right) = 4? - {y^2}$;

c)      ${x^2} + 8xy + ? = {\left( {? + 4y} \right)^2}$;

d)      $? - 12xy + 9{y^2} = {\left( {2x - ?} \right)^2}$.

Bài 2 :

Tính nhanh:

a)      $54.66$;

b)      ${203^2}$.

Bài 3 :

Rút gọn các biểu thức sau:

a)      ${\left( {x - 3y} \right)^2} - {\left( {x + 3y} \right)^2}$

b)      ${\left( {3x + 4y} \right)^2} + {\left( {4x - 3y} \right)^2}$

Bài 4 :

Rút gọn biểu thức

${\left( {x - y} \right)^3} + {\left( {x + y} \right)^3}$.

Bài 5 :

Khai triển:

a)      ${\left( {{x^2} + 2y} \right)^3}$;

b)      ${\left( {\dfrac{1}{2}x - 1} \right)^3}$.

Bài 6 :

Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu.

a)      $27 + 54x + 36{x^2} + 8{x^3}$.

b)      $64{x^3} - 144{x^2}y + 108x{y^2} - 27{y^3}$.

Bài 7 :

Tính nhanh giá trị của biểu thức:

a)      ${x^3} + 9{x^2} + 27x + 27$ tại x=7.

b)      $27 - 54x + 36{x^2} - 8{x^3}$ tại x=6,5.

Bài 8 :

Rút gọn các biểu thức sau:

a)      ${\left( {x - 2y} \right)^3} + {\left( {x + 2y} \right)^3}$

b)      ${\left( {3x + 2y} \right)^3} + {\left( {3x - 2y} \right)^3}$

Bài 9 :

Viết các biểu thức sau dưới dạng tổng hay hiệu hai lập phương:

a)      $\left( {x + 4} \right)\left( {{x^2} - 4x + 16} \right)$;

b)      $\left( {4{x^2} + 2xy + {y^2}} \right)\left( {2x - y} \right)$

Bài 10 :

Thay ? bằng biểu thức thích hợp.

a)      ${x^3} + 512 = \left( {x + 8} \right)\left( {{x^2} - ? + 64} \right)$;

b)      $27{x^3} - 8{y^3} = \left( {? - 2y} \right)\left( {? + 6xy + 4{y^2}} \right)$.

Bài 11 :

Viết các đa thức sau dưới dạng tích:

a)      $27{x^3} + {y^3}$;

b)      ${x^3} - 8{y^3}$.

Bài 12 :

Rút gọn biểu thức sau:

$\left( {x - 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right) + \left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right)$.

Bài 13 :

Tính nhanh giá trị của các biểu thức:

a)      ${x^3} + 3{x^2} + 3x + 1$ tại x=99.

b)      ${x^3} - 3{x^2}y + 3x{y^2} - {y^3}$ tại x=88 và y=-12.

Bài 14 :

Rút gọn biểu thức sau:

a)      ${\left( {x - 2} \right)^3} + {\left( {x + 2} \right)^3} - 6x\left( {x + 2} \right)\left( {x - 2} \right)$

b)      ${\left( {2x - y} \right)^3} + {\left( {2x + y} \right)^3}$.

Bài 15 :

Rút gọn  biểu thức $A = {\left( {2x + 1} \right)^3} - 6x\left( {2x + 1} \right)$ ta được

A. ${x^3} + 8$

B. ${x^3} + 1$

C. $8{x^3} + 1$

D. $8{x^3} - 1$

Bài 16 :

Tính nhanh giá trị của các biểu thức:

a)      ${x^2} - 4x + 4$ tại x=102.

b)      ${x^3} + 3{x^2} + 3x + 1$ tại x=999.

Bài 17 :

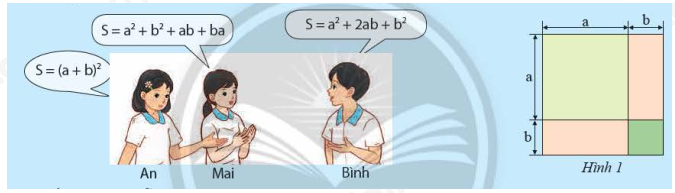
a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích $S$ của các phần tô màu trong Hình 1 như sau:

Kết quả của mỗi bạn có đúng không? Giải thích.

b) Thực hiện phép nhân và rút gọn đa thức của bạn An.

c) Bằng cách làm tương tự ở câu b), có thể biến đổi biểu thức ${\left( {a - b} \right)^2}$ thành biểu thức nào?

Bài 18 :

Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:

a) ${a^2} + 10ab + 25{b^2}$                                               

b) $1 + 9{a^2} - 6a$

Bài 19 :

Tính nhanh:

a) ${52^2}$                                                               

b) ${98^2}$

Bài 20 :

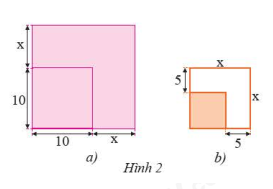
a) Một mảnh vườn hình vuông có cạnh $10$m được mở rộng cả hai cạnh thêm $x$ (m) như Hình 2a. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn sau khi mở rộng.

b) Một mảnh vườn hình vuông sau khi mở rộng mỗi cạnh $5$m thì được một mảnh vườn hình vuông có cạnh là $x$ (m) như Hình 2b. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn trước khi mở rộng.

Bài 21 :

Tính:

a) ${\left( {x + 2y} \right)^3}$                                             

b) ${\left( {3y - 1} \right)^3}$

Bài 22 :

Hoàn thành các phép nhân đa thức sau vào vở, thu gọn kết quả nhận được:

$\begin{array}{l}{\left( {a + b} \right)^3} = \left( {a + b} \right){\left( {a + b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\;\; = ...\end{array}$                                   $\begin{array}{l}{\left( {a - b} \right)^3} = \left( {a - b} \right){\left( {a - b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\;\; = ...\end{array}$

Bài 23 :

Sử dụng quy tắc chuyển vế và các tính chất của phép toán, hoàn thành các biến đổi sau vào vở:

$\begin{array}{l}{\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\\{a^3} + {b^3} = {\left( {a + b} \right)^3} - 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\; = ...\end{array}$                      $\begin{array}{l}{\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\\{a^3} - {b^3} = {\left( {a - b} \right)^3} + 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a - b} \right)^3} + 3ab\left( {a - b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\; = ...\end{array}$

Bài 24 :

Viết các đa thức sau dưới dạng tích:

a) $8{y^3} + 1$                                 

b) ${y^3} - 8$

Bài 25 :

Tính:

a) $\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)$                                             

b) $\left( {2x - \dfrac{1}{2}} \right)\left( {4{x^2} + x + \dfrac{1}{4}} \right)$

Bài 26 :

Tính:

a) ${\left( {3x + 4} \right)^2}$                                 

b) ${\left( {5x - y} \right)^2}$                                  

c) ${\left( {xy - \dfrac{1}{2}y} \right)^2}$

Bài 27 :

Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:

a) ${x^2} + 2x + 1$              

b) $9 - 24x + 16{x^2}$                     

c) $4{x^2} + \dfrac{1}{4} + 2x$

Bài 28 :

a) Viết biểu thức tính diện tích của hình vuông có cạnh bằng $2x + 3$ dưới dạng đa thức

b) Viết biểu thức tính thể tích của khối lập phương có cạnh bằng $3x - 2$ dưới dạng đa thức.

Bài 29 :

Tính nhanh:

a) $38.42$                               b) ${102^2}$                          c) ${198^2}$              d) ${75^2} - {25^2}$

Bài 30 :

Viết các biểu thức sau thành đa thức:

a) ${\left( {2x - 3} \right)^3}$                                  

b) ${\left( {a + 3b} \right)^3}$                                 

c) ${\left( {xy - 1} \right)^3}$