Nội dung từ Loigiaihay.Com
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 5
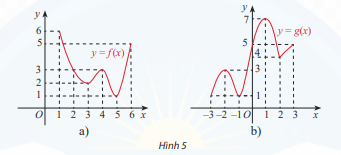
Quan sát đồ thị, xác định giá trị lớn nhất và giá trị nhỏ nhất bằng cách:
- Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu f(x) \( \le \) M với mọi x thuộc D và tồn tại \({x_0}\) thuộc D sao cho f(\({x_0}\)) = M. Kí hiệu M = \(\mathop {\max }\limits_D \)f(x). Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu f(x) \( \ge \) m với mọi x thuộc D và tồn tại \({x_0}\) thuộc D sao cho f(\({x_0}\)) = m. Kí hiệu m = \(\mathop {\min }\limits_D \)f(x).
a) Từ đồ thị, ta thấy \(\mathop {\max }\limits_{[1;6]} f(x) = f(1) = 6\) và \(\mathop {\min }\limits_{[1;6]} f(x) = f(5) = 1\)
b) Từ đồ thị, ta thấy \(\mathop {\max }\limits_{[ - 3;3]} g(x) = g( - 3) = g( - 1) = 1\) và \(\mathop {\min }\limits_{[ - 3;3]} g(x) = g(1) = 7\)

Các bài tập cùng chuyên đề
Bài 1 :
Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M = - 2$. Chọn khẳng định đúng:
-
A.
$f\left( x \right) \geqslant - 2,\forall x \in \left[ {1;3} \right]$
-
B.
$f\left( 1 \right) = f\left( 3 \right) = - 2$
-
C.
$f\left( x \right) < - 2,\forall x \in \left[ {1;3} \right]$
-
D.
$f\left( x \right) \leqslant - 2,\forall x \in \left[ {1;3} \right]$
Bài 2 :
Cho hàm số \(y = {x^2}\), biết \({x^2} \ge 0,\forall x \in R\) và \({x^2} = 0 \Leftrightarrow x = 0 \Rightarrow y = 0\). Khi đó \(y = 0\) là:
-
A.
GTNN của hàm số.
-
B.
GTLN của hàm số.
-
C.
GTNN của đồ thị hàm số.
-
D.
GTLN của đồ thị hàm số.
Bài 3 :
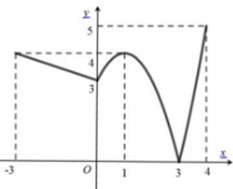
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 3;4} \right]\) và có đồ thị như hình vẽ bên. Gọi \(M\) và \(m\) lần lượt là các giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 3;4} \right]\). Tính \(M + m\).
-
A.
5
-
B.
8
-
C.
7
-
D.
1
Bài 4 :
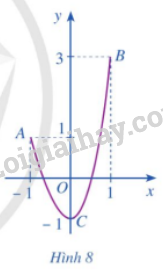
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;1} \right]\) và có đồ thị là đường cong ở Hình 8. Quan sát đồ thị và cho biết:
a) Điểm nào thuộc đồ thị hàm số có tung độ lớn nhất
b) Điểm nào thuộc đồ thị hàm số có tung độ nhỏ nhất
Bài 5 :
Nếu hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) thỏa mãn \(f'\left( x \right) = \sin x - 2023,\forall x \in \mathbb{R}\) thì giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {1;2} \right]\) bằng:
A. \(f\left( 0 \right)\).
B. \(f\left( 1 \right)\).
C. \(f\left( {1,5} \right)\).
D. \(f\left( 2 \right)\).
Bài 6 :
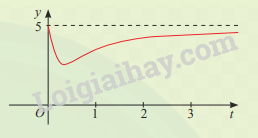
Sự phân huỷ của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (t \( \ge \) 0) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số (có đồ thị như đường màu đỏ ở hình bên)
\(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\)
Vào các thời điểm nào nồng độ oxygen trong nước cao nhất và thấp nhất?
(Theo: https://www.researchgate.net/publication/264903978_Microrespirometric_ characterization _of_activated_sludge_inhibition_by_copper_and_zinc)
Bài 7 :
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) \(f(x) = 2{x^3} - 9{x^2} + 12x + 1\) trên đoạn [0;3]
b) \(g(x) = x + \frac{1}{x}\) trên khoảng (0;5)
c) \(h(x) = x\sqrt {2 - {x^2}} \)
Bài 8 :
Hình 1 cho biết sự thay đổi của nhiệt độ ở một thành phố trong một ngày.
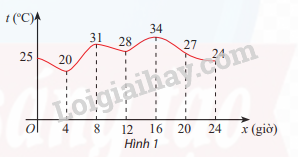
a) Khẳng định nào sau đây đúng? Vì sao?
i) Nhiệt độ cao nhất trong ngày là \(28^\circ C\).
ii) Nhiệt độ cao nhất trong ngày là \(40^\circ C\).
iii) Nhiệt độ cao nhất trong ngày là \(34^\circ C\).
b) Hãy xác định thời điểm có nhiệt độ cao nhất trong ngày.
c) Nhiệt độ thấp nhất trong ngày là bao nhiêu?
Bài 9 :
Cho hàm số f(x) có đồ thị như hình dưới đây:
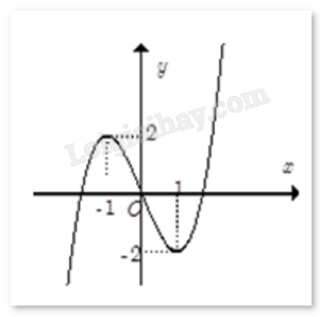
Giá trị lớn nhất của hàm số đã cho trên [-1;1] là:
-
A.
y = 2
-
B.
y = 1
-
C.
x = 2
-
D.
y = 0
Bài 10 :
Cho hàm số f(x) có đồ thị như hình dưới đây:
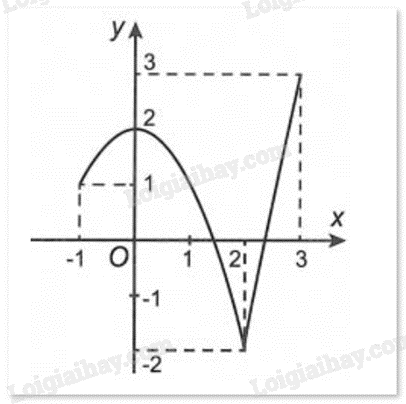
Giá trị lớn nhất của hàm số đã cho trên [-1;3] là:
-
A.
y = 1
-
B.
y = 2
-
C.
y = -2
-
D.
y = 3
Bài 11 :
Cho hàm số y = f(x) liên tục trên đoạn [–1;2] và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [–1;2]. Tính M + 2m.
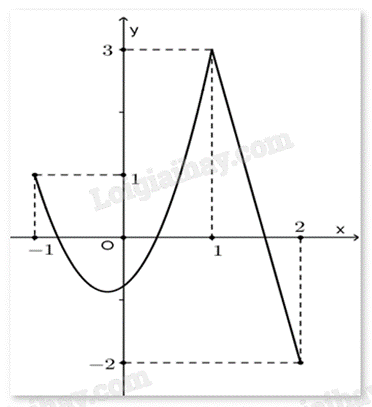
-
A.
y = 2
-
B.
y = -1
-
C.
y = 0
-
D.
y = 1
Bài 12 :
Cho hàm số y = f(x) liên tục trên đoạn [−1;4] và có đồ thị như hình vẽ dưới đây.

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [–1;4]. Tính M + m.
-
A.
4
-
B.
3
-
C.
2
-
D.
1
Bài 13 :
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
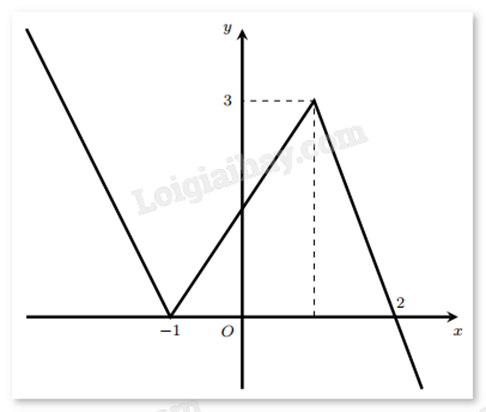
Tìm giá trị lớn nhất của hàm số g(x) = 2f(x) – 1trên đoạn [–1;2].
-
A.
3
-
B.
4
-
C.
5
-
D.
6
Bài 14 :
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
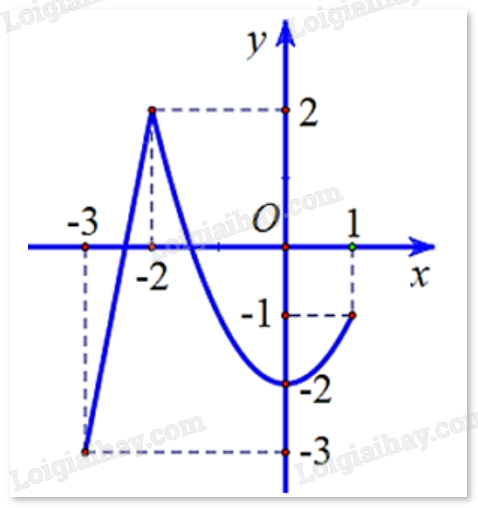
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-3;1]. Tính M + m.
-
A.
-1
-
B.
-2
-
C.
0
-
D.
-3
Bài 15 :
Một doanh nghiệp dự kiến lợi nhuận khi sản xuất x sản phẩm (\(0 \le x \le 300\)) được cho bởi hàm số \(y = - {x^3} + 300{x^2}\) (đơn vị: đồng) và được minh họa bằng đồ thị ở hình bên dưới.
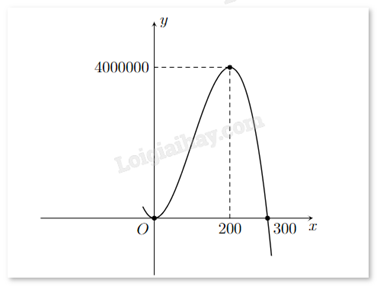
Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận dự kiến thu được nhiều nhất?
-
A.
4000000
-
B.
200
-
C.
300
-
D.
150
Bài 16 :
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
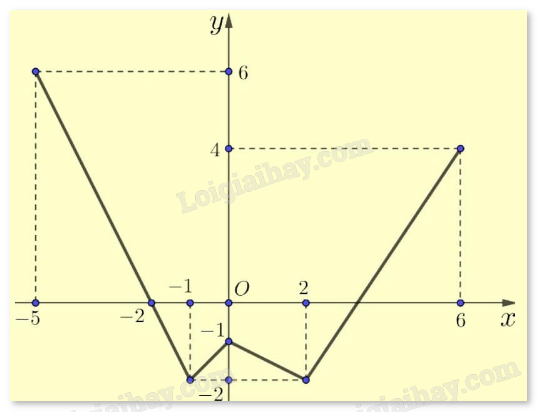
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2;2]. Tính M + m.
-
A.
-1
-
B.
-2
-
C.
0
-
D.
-3
Bài 17 :
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;2]. Tính M - m.
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Bài 18 :
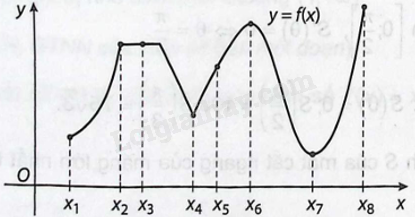
Sử dụng đồ thị dưới đây, xác định xem hàm số \(y = f\left( x \right)\) có giá trị lớn nhất, giá trị nhỏ nhất hay cực trị tại mỗi điểm \({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8}\) hay không.
Bài 19 :
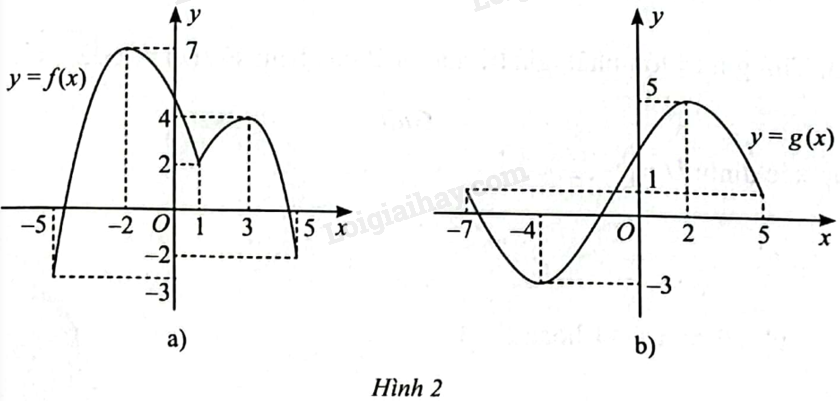
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 2.
Bài 20 :
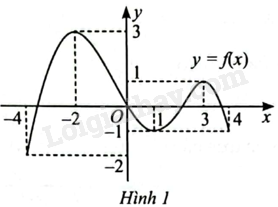
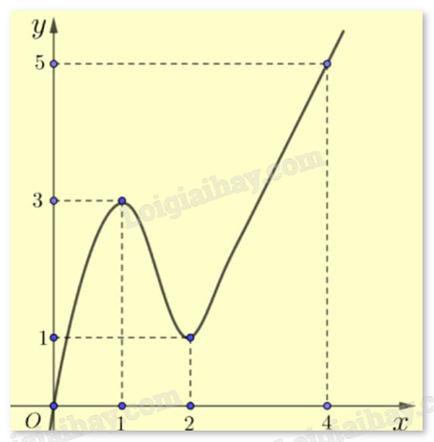
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {0;4} \right]\) trong Hình 1 là:
A. ‒1.
B. ‒2.
C. 0.
D. 1.
Bài 21 :
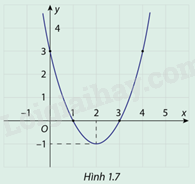
Cho hàm số \(y = f(x) = {x^2} - 4x + 3\) có đồ thị như hình 1.7
a) Tìm tọa độ điểm thấp nhất của đồ thị hàm số \(f(x)\) đã cho.
b) Khi \(x\) thay đổi trên đoạn \([1;4]\), tìm \({x_0} \in [1;4]\) để \(f({x_0})\) có giá trị lớn nhất.
Bài 22 :
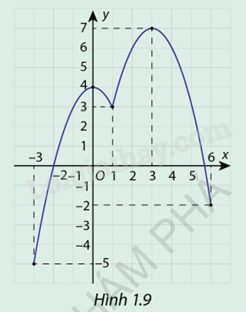
Cho hàm số \(y = f(x)\) liên tục trên đoạn, có đạo hàm trên các khoảng \(( - 3;1)\)và \((1;6)\) có dồ thị hàm số như hình 1.9, biết rằng \(f( - 3) = - 5\) và \(f(6) = - 2\).
a) Xác định các điểm cực trị thuộc đoạn \([ - 3;6]\) của hàm số.
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \([ - 3;6]\).
Bài 23 :
Cho hàm số f(x) có đồ thị như hình dưới.
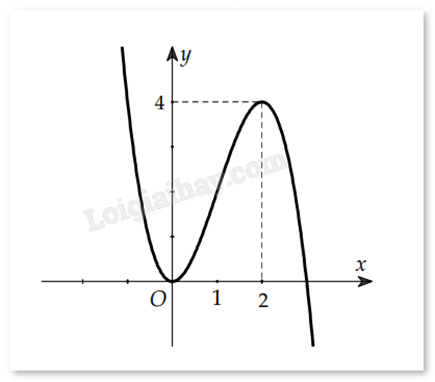
Giá trị lớn nhất của hàm số f(x) là
-
A.
1
-
B.
2
-
C.
4
-
D.
Đáp án khác
Bài 24 :
Cho hàm số f(x) có đồ thị như hình dưới.
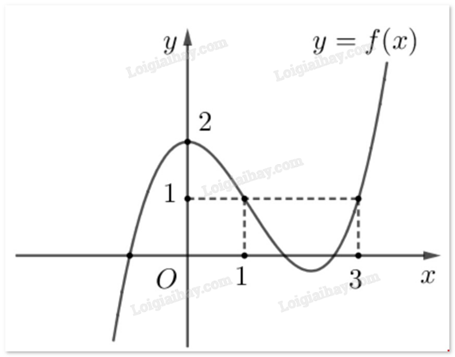
Giá trị lớn nhất của hàm số f(x) trên đoạn [0;3] là
-
A.
1
-
B.
2
-
C.
3
-
D.
0
Bài 25 :
Cho hàm số f(x) có bảng biến thiên như hình dưới.
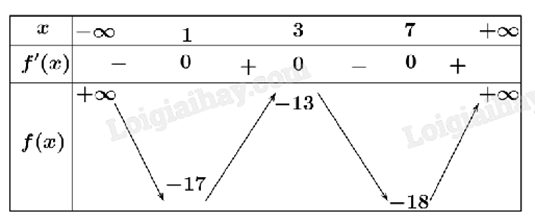
Giá trị nhỏ nhất của hàm số f(x) là
-
A.
-13
-
B.
-17
-
C.
-18
-
D.
7
Bài 26 :
Cho hàm số f(x) có đồ thị như hình dưới.
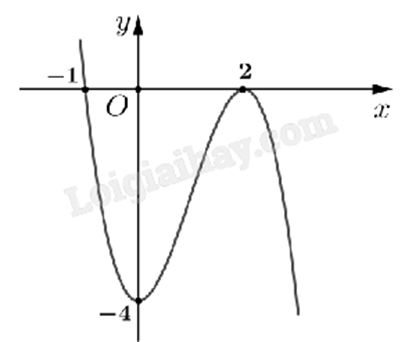
Giá trị nhỏ nhất của hàm số f(x) trên đoạn [0;2] là
-
A.
-1
-
B.
-4
-
C.
2
-
D.
0
Bài 27 :
Cho hàm số f(x) có đồ thị như hình dưới.
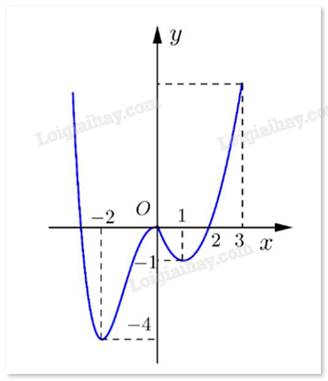
Giá trị nhỏ nhất của hàm số f(x) trên đoạn [0;3] là
-
A.
-1
-
B.
1
-
C.
2
-
D.
3
Bài 28 :
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ sau:
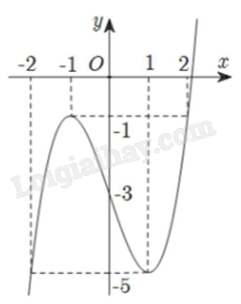
Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số đã cho trên đoạn [-2;2] bằng
-
A.
0
-
B.
-1
-
C.
-5
-
D.
-6
Bài 29 :
Cho hàm số y = f (x) có bảng biến thiên như hình bên. Giá trị lớn nhất của hàm số đã cho trên đoạn [-2;4] bằng
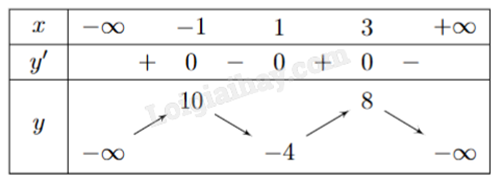
-
A.
-1
-
B.
10
-
C.
1
-
D.
8
Bài 30 :
Cho hàm số y = f(x) có bảng biến thiên như hình. Giá trị nhỏ nhất của hàm số y = f(x) trên [-1;1] bằng
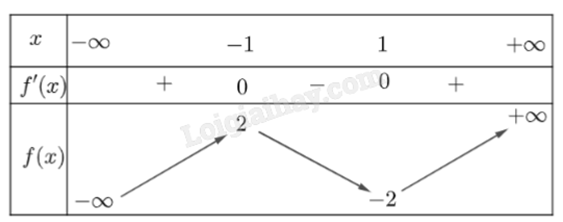
-
A.
-3
-
B.
-1
-
C.
-2
-
D.
1












