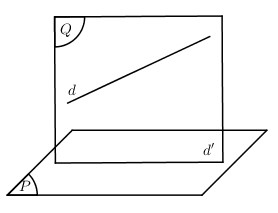
Giải bài 2 trang 89 SGK Hình học 12Viết phương trình tham số của đường thẳng là hình chiếu vuông góc của đường thẳng d trên các trục. Video hướng dẫn giải Viết phương trình tham số của đường thẳng là hình chiếu vuông góc của đường thẳng \(d\): \(\left\{\begin{matrix} x=2+t \\ y=-3+2t \\ z= 1+3t \end{matrix}\right.\) lần lượt trên các mặt phẳng sau: LG a a) \((Oxy)\) ; Phương pháp giải: Cách 1: Phương pháp viết phương trình hình chiếu \((d')\) của đường thẳng \((d)\) trên mặt phẳng \((P)\): Bước 1: Viết phương trình mặt phẳng \((Q)\) chứa \((d )\) và vuông góc với \((P\)). - \({\overrightarrow n _{\left( Q \right)}} = \left[ {{{\overrightarrow u }_{\left( d \right)}};{{\overrightarrow n }_{\left( P \right)}}} \right]\). - \(M \in d \Rightarrow M \in \left( Q \right)\) (với M là một điểm bất kì). Bước 2: \(d' = \left( P \right) \cap \left( Q \right)\). Viết phương trình đường thẳng \((d')\).
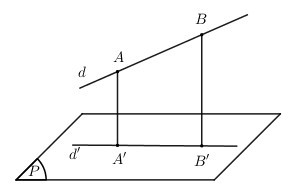
Cách 2: Lấy 2 điểm \(A,B\) bất kì thuộc d, gọi \(A',B'\) lần lượt là hình chiếu vuông góc của A, B trên (P). Khi đó \((d')\) chính là đường thẳng \(A'B'\).
Lời giải chi tiết: Gọi \(\left( P \right)\) là mặt phẳng vuông góc \(\left( {Oxy} \right)\) và chứa \(d\). Khi đó \(\Delta = \left( P \right) \cap \left( {Oxy} \right)\) là hình chiếu của \(d\) lên \(\left( {Oxy} \right)\). Phương trình mặt phẳng \((Oxy)\) có dạng: \(z = 0\); vectơ \(\overrightarrow{k}\)(0 ; 0 ;1) là vectơ pháp tuyến của \((Oxy)\). Ta có: \(\left\{ \begin{array}{l}\overrightarrow {{n_{\left( P \right)}}} \bot \overrightarrow k \\\overrightarrow {{n_{\left( P \right)}}} \bot \overrightarrow {{u_d}} \end{array} \right.\) \(\Rightarrow \overrightarrow{n_{(P)}}=\left [\overrightarrow{u},\overrightarrow{k} \right ] = (2 ; -1 ; 0)\) là vectơ pháp tuyến của \((P)\). Phương trình mặt phẳng \((P)\) có dạng: \(2(x - 2) - (y + 3) +0.(z - 1) = 0 \) \(\Leftrightarrow 2x - y - 7 = 0\). \(\Delta = \left( P \right) \cap \left( {Oxy} \right)\) \(\Rightarrow \Delta :\left\{\begin{matrix} z=0 & \\ 2x-y-7=0.& \end{matrix}\right.\) Chọn \({M_0}\left( {4;1;0} \right) \in \left( P \right) \cap \left( {Oxy} \right)\). \(\Delta = \left( P \right) \cap \left( {Oxy} \right)\) \( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{u_\Delta }} \bot \overrightarrow {{n_{\left( P \right)}}} \\\overrightarrow {{u_\Delta }} \bot \overrightarrow k \end{array} \right.\) \( \Rightarrow \overrightarrow {{u_\Delta }} = \left[ {\overrightarrow k ,\overrightarrow {{n_{\left( P \right)}}} } \right] = \left( {1;2;0} \right)\). Đường thẳng \(\Delta \) đi qua \({M_0}\left( {4;1;0} \right)\) và nhận \(\overrightarrow {{u_\Delta }} = \left( {1;2;0} \right)\) làm VTCP nên \(\Delta :\left\{ \begin{array}{l}x = 4 + t\\y = 1 + 2t\\z = 0\end{array} \right.,t \in \mathbb{R}\). Cách khác: +) t = 0 ⇒ điểm M(2; -3; 1) ∈ d +) t = 1 ⇒ điểm N(3; -1; 4) ∈ d. Hình chiếu của M trên (Oxy) là M’(2 ; -3 ; 0). Hình chiếu của N trên (Oxy) là : N’(3 ; -1 ; 0). ⇒ Hình chiếu của d trên (Oxy) là đường thẳng d’ đi qua M’ và N’. ⇒ d’ đi qua M'(2;-3;0) và nhận \(\overrightarrow {M'N'} = \left( {1;2;0} \right)\) là 1 vtcp. \(⇒ d':\left\{ \begin{array}{l} LG b b) \((Oyz)\). Lời giải chi tiết: Mặt phẳng \((Oyz)\) có phương trình \(x = 0\). Lấy \(M_1( 2 ;- 3 ; 1) ∈ d\) và \(M_2( 0 ; -7 ; -5) ∈ d\). +) Hình chiếu vuông góc của \(M_1\) trên \((Oyz)\) là \(M_1\)'\((0 ; -3 ; 1)\). +) Hình chiếu vuông góc của \(M_2\) trên \((Oyz)\) là chính nó. Đường thẳng \(∆\) qua \({M_1}',{M_2}\) chính là hình chiếu vuông góc của \(d\) lên \((Oyz)\). Ta có: \(\overrightarrow{M'_{1}M_{2}}(0 ; -4 ; -6)\) // \(\overrightarrow{v} (0 ; 2 ; 3)\). Phương trình \(M'_1M_2\) có dạng: \(\left\{\begin{matrix} x=0 & \\ y=-3+2t&,t \in R \\ z=1+3t& \end{matrix}\right.\). HocTot.XYZ
|