Nội dung từ Loigiaihay.Com
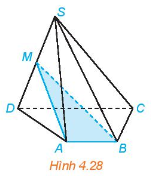
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28)
a) Xác định giao tuyến của hai mặt phẳng (MAB) và (SCD).
b) Gọi N là giao điểm của đường thẳng SC và mặt phẳng (MAB). Chứng minh rằng MN là đường trung bình của tam giác SCD.
Để xác định giao tuyến của hai mặt phẳng, ta tìm hai điểm chung thuộc cả hai mặt phẳng đó
Để xác định giao điểm của một đường thẳng và một mặt phẳng, ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.
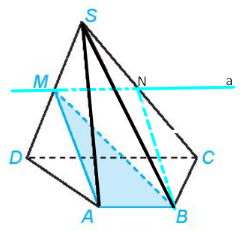
a) mp(MAB) và (SCD)có điểm M chung và chứa hai đường thẳng thẳng song song là AB và CD
Do đó giao tuyến của hai mặt phẳng (MAB) và (SCD) là đường thẳng a đi qua M và song song với CD, AB.
b, Do MN //CD và M là trung điểm của SD.
Suy ra, MN là đường trung bình của tam giác SCD.

Các bài tập cùng chuyên đề
Bài 1 :
Cho tứ diện ABCD. Gọi \(P,Q\) lần lượt là trung điểm của các cạnh \(AB,CD\). Lấy điểm \(R\) trên cạnh \(BC\) sao cho BR = 2RC. Gọi S là giao điểm của AD với mặt phẳng (PQR). Khi đó tỉ số \(\frac{{SA}}{{SD}}\) bằng?
-
A.
\(2\)
-
B.
\(\frac{1}{3}\)
-
C.
\(\frac{5}{3}\)
-
D.
\(\frac{3}{2}\)
Bài 2 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD và G là trọng tâm tam giác SBD. Mặt phẳng (MNG) cắt SC tại điểm H. Khi đó tỉ số \(\frac{{SH}}{{SC}}\) bằng?
-
A.
\(\frac{1}{3}\)
-
B.
\(\frac{1}{2}\)
-
C.
\(\frac{2}{5}\)
-
D.
\(3\)
Bài 3 :
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC.
a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (BPD).
b) Chứng minh rằng d song song với BD.
Bài 4 :
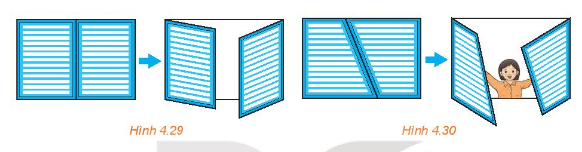
(Đố vui) Khi hai cánh cửa sổ hình chữ nhật được mở, dù ở vị trí nào, thì hai mép ngoài của chúng luôn song song với nhau (H.4.29). Hãy giải thích tại sao?
Nếu hai cánh cửa sổ có dạng hình thang như Hình 4.30 thì có vị trí nào của hai cánh cửa để hai mép ngoài của chúng song song với nhau hay không?
Bài 5 :
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, \(AC\) và \(BD\) cắt nhau tại \(O\). Gọi \(I\) là trung điểm của \(SO\). Mặt phẳng \(\left( {ICD} \right)\) cắt \(SA,SB\) lần lượt tại \(M,N\).
a) Hãy nói cách xác định hai điểm \(M\) và \(N\). Cho \(AB = a\). Tính \(MN\) theo \(a\).
b) Trong mặt phẳng \(\left( {CDMN} \right)\), gọi \(K\) là giao điểm của \(CN\) và \(DM\). Chứng minh \(SK\parallel BC\parallel AD\).
Bài 6 :
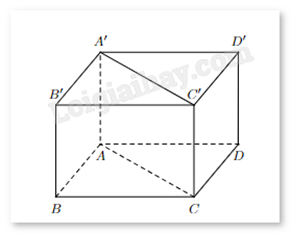
Cho hình hộp chữ nhật ABCD.A’B’C’D’ như hình. Mệnh đề nào sau đây là sai?
-
A.
AB//CD
-
B.
AB//C’D’
-
C.
AB//A’B’
-
D.
AB//A’C’
Bài 7 :
Cho tứ diện ABCD, M thuộc đoạn AB, thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\) đi qua M song song với BD và AC là hình có mấy cạnh?
Bài 8 :
-
A.
$EF$
-
B.
$DC$
-
C.
$AD$
-
D.
$AB$
Bài 9 :
Trong không gian, cho ba đường thẳng phân biệt $a,\,\,b,\,\,c$ trong đó $a\,{\text{//}}\,b$. Khẳng định nào sau đây sai?
-
A.
Nếu $a\,{\text{//}}\,c$ thì $b\,{\text{//}}\,c$.
-
B.
Nếu $c$ cắt $a$ thì $c$ cắt $b$.
-
C.
Nếu $A \in a$ và $B \in b$ thì ba đường thẳng $a,\,\,b,\,\,AB$ cùng ở trên một mặt phẳng.
-
D.
Tồn tại duy nhất một mặt phẳng qua $a$ và $b$.
Bài 10 :
Cho hình chóp tứ giác \(S.ABCD\). Gọi \(G\), \(K\) lần lượt là trọng tâm của các tam giác \(SAB\) và \(SAD\); \(M\), \(N\) lần lượt là trung điểm của các cạnh \(BC\) và \(CD\). Chứng minh rằng \(GK\parallel MN\).
Bài 11 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I\), \(J\),\(K\), \(L\) lần lượt là trọng tâm của các tam giác \(SAB\), \(SBC\), \(SCD\), \(SAD\).
a) Chứng minh rằng bốn điểm \(I\), \(J\),\(K\), \(L\) đồng phẳng và tứ giác \(IJKL\) là hình bình hành.
b) Chứng minh rằng \(JL\parallel {\rm{CD}}\).
c) Xác định giao tuyến của hai mặt phẳng \(\left( {IJKL} \right)\) và \(\left( {SCD} \right)\).
Bài 12 :
Cho tứ diện \(ABCD\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(AB\), \(AD\); \(P\), \(Q\) lần lượt thuộc các cạnh \(CD\), \(BC\) (\(P\), \(Q\) không trùng với \(B\), \(C\), \(D\)). Chứng minh rằng nếu \(M\), \(N\), \(P\), \(Q\) cùng thuộc một mặt phẳng thì \(PQ\) song song với \(BD\).
Bài 13 :
Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Xác định giao tuyến của hai mặt phẳng (ANP) và (CMQ).
b) Xác định giao tuyến của hai mặt phẳng (ANP) và (ABD).
c) Xác định giao tuyến của hai mặt phẳng (CMQ) và (BCD).
d) Chứng minh rằng các giao tuyến ở trên đôi một song song với nhau.
Bài 14 :
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi G, H lần lượt là giao điểm của hai đường chéo của hai hình bình hành đó. Chứng minh rằng ba đường thẳng GH, CE, DF đôi một song song.
Bài 15 :
Cho hình chóp ngũ giác S.ABCDE. Giả sử AB song song với DE.
a) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBE).
b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SDE).
c) Giả sử giao tuyến của hai mặt phẳng (SAE) và (SBC) song song với đường thẳng AE. Chứng minh AE//BC
Bài 16 :
Cho tứ diện \(ABCD.\) Gọi \(I,\,\,J\) lần lượt là trọng tâm của các tam giác \(ABC\) và \(ABD.\) Khẳng định nào sau đây đúng?
-
A.
\(IJ\) cắt \(AB.\)
-
B.
\(IJ\) song song \(AB.\)
-
C.
\(IJ\) và \(CD\) là hai đường thẳng chéo nhau.
-
D.
\(IJ\) song song \(CD.\)
Bài 17 :
Cho tứ diện $ABCD.$ Gọi $M,\,N$ lần lượt là các điểm thuộc các cạnh $AB,\,AC$ sao cho $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$; $I,\,J$ lần lượt là trung điểm của $BD$ và $CD.$
Khẳng định nào sau đây đúng?
-
A.
$IJ$ cắt $BC.$
-
B.
$IJ$ song song $MN.$
-
C.
$IJ$ và $MN$ là hai đường thẳng chéo nhau.
-
D.
$IJ$ và $MN$ là hai đường thẳng song song hoặc chéo nhau.
Bài 18 :
Cho hình chóp S.ABCD có ABCD là hình thang với hai cạnh đáy là AD và BC, đáy lớn là AD. Gọi M, N là lần lượt là trung điểm của SA và SD.
a) MN//BC.
b) Giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song với AD.
c) Gọi \(AB \cap CD = \{ E\} \), \(\{ F\} = SB \cap ME\). Khi đó \(SB \cap (MCD) = \{ F\} \).
d) Giao tuyến của (SAB) và (SCD) là đường thẳng qua S và song song với AB.
Bài 19 :
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB và BC. P là điểm thuộc CD sao cho PD = 2PC. Gọi Q là giao diểm của đường thẳng AD và mặt phẳng (MNP). Tính tỉ số \(\frac{{AQ}}{{AD}}\) (làm tròn đến hàng phần trăm).
Bài 20 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC). Gọi M là trung điểm của BC, N là điểm thuộc cạnh SC sao cho \(\frac{{SN}}{{SC}} = \frac{1}{4}\). Gọi E là giao điểm của MN và d, F là giao điểm của AE và SD. Tính tỉ số \(\frac{{{S_{FDA}}}}{{{S_{FSE}}}}\)?
Bài 21 :
Cho tứ diện ABCD có I, J lần lượt là trung điểm của các cạnh BC và BD. Gọi (P) là mặt phẳng qua I, J và cắt hai cạnh AC và AD lần lượt tại M và N. Để IJNM là hình thoi thì AC = kAM và AB = mCD. Khi đó giá trị của k + m bằng bao nhiêu?
Bài 22 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA và SC. Đường thẳng MN song song với đường thẳng nào dưới đây?
-
A.
BC.
-
B.
BD.
-
C.
AB.
-
D.
AC.
Bài 23 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của SA, SB, AB.

Đường thẳng nào sau đây song song với đường thẳng CD?
-
A.
AN.
-
B.
MN.
-
C.
MP.
-
D.
NP.
Bài 24 :
Cho hình chóp $S.ABCD$ có đáy là hình thang, $AB\,\text{//}\, CD$ và $AB = 2CD$, O là giao điểm của hai đường thẳng AC và BD. Gọi $M$, $N$ lần lượt là trung điểm $SA$ và $SB$.
a) $AB\,\text{//}\, MC$.
b) Tứ giác CDMN là hình thang cân.
c) E là trung điểm của SC, G là trọng tâm của tam giác SBC, khi đó OG song song với DE.
d) Giao tuyến của (CDE) và (SAC) là đường thẳng EO.
Bài 25 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm của SC.

a) SO là giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Giao điểm của đường thẳng AM và mặt phẳng (SBD) thuộc cạnh SO.
c) Đường thẳng MO cắt mặt phẳng (SAD).
d) Ba mặt phẳng (SAB), (SAC) và (MOB) đôi một cắt nhau theo ba giao tuyến phân biệt và ba giao tuyến này đồng quy.
Bài 26 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số \(\frac{{SK}}{{SC}}\) bằng bao nhiêu?












