Nội dung từ Loigiaihay.Com
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng đường thẳng MN song song với giao tuyến d của hai mặt phẳng (SBC) và (SAD).
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b song song với a
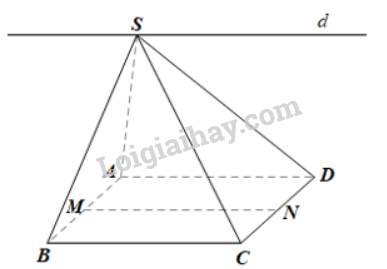
Ta có: S ∈ (SAD) và S ∈ (SBC) nên S là giao điểm của (SAD) và (SBC).
Lại có: AD // BC (do ABCD là hình bình hành);
AD ⊂ (SAD);
BC ⊂ (SBC).
Do đó giao tuyến d của hai mặt phẳng (SAD) và (SBC) là đường thẳng đi qua S và song song với AD, BC.
Vì M, N lần lượt là trung điểm của AB và CD nên MN là đường trung bình
Do đó MN // BC // AD.
Ta có: MN // BC mà BC ⊂ (SBC) nên MN // (SBC);
MN // AD mà AD ⊂ (SAD) nên MN // (SAD).
Có: MN // (SBC);
MN // (SAD);
(SAD) ∩ (SBC) = d
Suy ra MN // d.

Các bài tập cùng chuyên đề
Bài 1 :
Cho các mệnh đề sau:
a) Nếu a // (P) thì a song song với mọi đường thẳng nằm trong (P).
b) Nếu a // (P) thì a song song với một đường thẳng nào đó nằm trong (P).
c) Nếu a // (P) thì có vô số đường thẳng nằm trong (P) và song song với a
d) Nếu a // (P) thì tồn tại đường thẳng d nằm trong (P) sao cho a và d đồng phẳng.
Số mệnh đề đúng là:
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Bài 2 :
Cho một điểm A nằm ngoài mặt phẳng (P). Có bao nhiêu đường thẳng qua A và song song với (P)?
-
A.
0.
-
B.
1.
-
C.
2.
-
D.
Vô số.
Bài 3 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của AB, CD, SA. Trong các mệnh đề sau, mệnh đề nào đúng?
-
A.
MP // SD
-
B.
SD // (MNP)
-
C.
MN // SC
-
D.
SC // (MNP)
Bài 4 :
Trong Ví dụ 4, gọi (Q) là mặt phẳng qua E và song song với hai đường thẳng AB, AD. Xác định giao tuyến của (Q) với các mặt của tứ diện.
Bài 5 :
Cho đường thẳng a song song với mặt phẳng (P) và (Q) là một mặt phẳng chứa a. Giả sử (Q) cắt (P) theo giao tuyến b (H. 4.36)
a) Hai đường thẳng a và b có thể chéo nhau không?
b) Hai đường thẳng a và b có thể cắt nhau không?

Bài 6 :
Trong tình huống mở đầu, hãy giải thích tại sao dây nhợ khi căng thì song song với mặt đất. Tác dụng của việc đó là gì?
Bài 7 :
Cho hình chóp S.ABCD có đáy là hình thang (AB//CD). Hai đường thẳng SD và AB có chéo nhau hay không? Chỉ ra mặt phẳng chứa đường thẳng SD và song song với AB.
Bài 8 :
Trong Ví dụ 2, chứng minh rằng đường thẳng c song song với mp(a,b), đường thẳng b song song với mp(a,c).
Bài 9 :
Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng b nằm trong (P). Gọi (Q) là mặt phẳng chứa a và b (H.4.36).
Nếu a và (P) cắt nhau tại điểm M thì M có thuộc (Q) và M có thuộc b hay không? Hãy rút ra kết luận sau khi trả lời các câu hỏi trên.
Bài 10 :
Trong không gian, cho hai đường thẳng phân biệt a, b và mặt phẳng (P). Những mệnh đề nào sau đây là đúng?
a) Nếu a và (P) có điểm chung thì a không song song với (P)
b) Nếu a và (P) có điểm chung thì a và (P) cắt nhau
c) Nếu a song song với b và b nằm trong (P) thì a song song với (P)
d) Nếu a và b song song với (P) thì a song song với b
Bài 11 :
Cho tam giác ABC và ABD không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trung điểm của các cạnh AC, AD
a) Đường thẳng AM có song song với mặt phẳng (BCD) hay không? Hãy giải thích tại sao.
b) Đường thẳng MN có song song với mặt phẳng (BCD) hay không? Hãy giải thích tại sao.
Bài 12 :
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của hai cạnh BC, CD. Chứng minh rằng đường thẳng BD song song với mặt phẳng (AMN).
Bài 13 :
Cho hình chóp S.ABCD có đáy là hình thang (AB//CD). Gọi E là một điểm nằm giữa S và A. Gọi (P) là mặt phẳng qua E và song song với hai đường thẳng AB, AD. Xác định giao tuyến của (P) và các mặt bên của hình chóp. Hình tạo bởi các giao tuyến là hình gì?
Bài 14 :
Bạn Nam quan sát thấy dù cửa ra vào được mở ở vị trí nào thì mép trên của cửa luôn song song với một mặt phẳng cố định. Hãy cho biết đó là mặt phẳng nào và giải thích tại sao.

Bài 15 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Đường thẳng SB song song với mặt phẳng
A. (CDM)
B. (ACM)
C. (ADM)
D. (ACD)
Bài 16 :
Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng a cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, C sao cho \(\frac{{AB}}{{BC}} = \frac{2}{3}\) và đường thẳng b cắt các mặt phẳng (P), (Q), (R) lần lượt tại A’, B’, C’. Tỉ số \(\frac{{A'B'}}{{B'C'}}\) bằng
A. \(\frac{2}{3}\)
B. \(\frac{1}{2}\)
C. \(\frac{3}{2}\)
D. \(\frac{2}{5}\)
Bài 17 :
Ở Ví dụ 3, xác định giao tuyến của mặt phẳng (R) với các mặt phẳng (ABD), (BCD), (ACD).
Bài 18 :
Cho hai mặt phẳng (P), (Q) cùng song song với đường thẳng a và (P) ∩ (Q) = b (Hình 54).
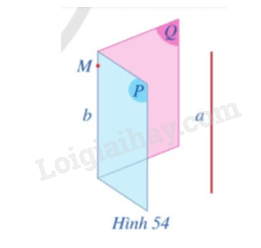
a) Lấy một điểm M trên đường thẳng b. Gọi b’, b” lần lượt là các giao tuyến của mặt phẳng (M, a) với (P) và mặt phẳng (M, a) với (Q). Cho biết b’ và b” có trùng với b hay không.
b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?
Bài 19 :
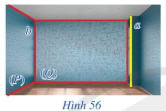
Trong Hình 56, hai mặt tường của căn phòng gợi nên hình ảnh hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến b, mép cột gợi nên hình ảnh đường thẳng a. Cho biết đường thẳng a có song song với giao tuyến b hay không.
Bài 20 :
Cho đường thẳng a song song với mặt phẳng (P). Cho mặt phẳng (Q) chứa a và cắt (P) theo giao tuyển b. (Hình 51)
a) Giả sử a cắt b tại M. Đường thẳng a có cắt mặt phẳng (P) tại M hay không?
b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?

Bài 21 :
Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD. Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD) không? Vì sao?
Bài 22 :
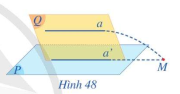
Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) (Hình 48). Gọi (Q) là mặt phẳng xác định bởi hai đường thẳng song song a, a’.
a) Giả sử a cắt (P) tại M. Đường thẳng a có cắt đường thẳng a’ tại M hay không?
b) Nêu vị trí tương đối của đường thẳng a và mặt phẳng (P). Vì sao?
Bài 23 :
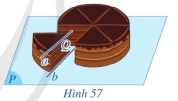
Trong Hình 57, khi cắt bánh sinh nhật, mặt cắt và mặt khay đựng bánh lần lượt gợi nên hình ảnh mặt phẳng (Q) và mặt phẳng (P); mép trên và mép dưới của lát cắt lần lượt gợi nên hình ảnh hai đường thẳng a và b trong đó a song song với mặt phẳng (P). Cho biết hai đường thẳng a, b có song song với nhau hay không.
Bài 24 :
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho \(BI = 2IC\). Chứng minh rằng IG song song với mặt phẳng (ACD).
Bài 25 :
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trọng tâm của hai tam giác ABF và ABC. Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACF).
Bài 26 :
Cho hình chóp S.ABCD có đáy là ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao cho \(AD = 3AM\). Gọi G, N lần lượt là trọng tâm của tam giác SAB, ABC.
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Chứng minh rằng MN song song với mặt phẳng (SCD) và NG song song với mặt phẳng (SAC).
Bài 27 :
Cho hai mặt phẳng (P) và (Q) song song với nhau. Đường thẳng a cắt hai mặt phẳng trên theo thứ tự tại A, B. Đường thẳng b song song với đường thẳng a và cắt hai mặt phẳng (P) và (Q) lần lượt tại A’, B’. Chứng minh rằng \(AB = A'B'\)
Bài 28 :
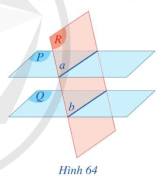
Cho hai mặt phẳng song song (P) và (Q). Mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a.
a) Mặt phẳng (R) có cắt mặt phẳng (Q) theo giao tuyến b, hãy nêu nhận xét về vị trí tương đối giữa hai giao tuyến a và b (Hình 64)
b) Trong trường hợp mặt phẳng (R) cắt mặt phẳng (Q) theo giao tuyến b, hãy nêu nhận xét về vị trí tương đối giữa hai giao tuyến a và b (Hình 64)
Bài 29 :
Trong không gian, đường thẳng song song với mặt phẳng khi và chỉ khi:
A. Đường thẳng đó song song với một đường thẳng thuộc mặt phẳng
B. Đường thẳng và mặt phẳng không có điểm chung
C. Đường thẳng đó không có điểm chung với một đường thẳng thuộc mặt phẳng
D. Đường thẳng đó không có điểm chung với hai đường thẳng thuộc mặt phẳng.
Bài 30 :
Hãy chỉ ra trong Hình 9 các đường thẳng lần lượt nằm trong, song song, cắt mặt phẳng sàn nhà.













